Try Statistical Software for Free
What is fit regression model?
A fit regression model is a statistical tool used to analyze the relationship between a dependent variable and one or more independent variables. A "fit" regression model is one that has been carefully chosen and adjusted to best represent the relationship between the variables of interest.
The process of fitting a regression model typically involves choosing the appropriate type of regression (linear, polynomial, logistic, etc.), selecting the most relevant independent variables, and adjusting the model parameters to minimize the difference between the predicted values and the actual observed values.
When to use fit regression model?
A fitted regression model is typically used when there is a need to analyze the relationship between one or more independent variables and a dependent variable. It is a useful tool for predicting and understanding the behavior of a dependent variable based on the values of the independent variables.
Here are some common scenarios where a fitted regression model may be useful:
- Predictive modeling: If you want to predict the value of a dependent variable based on the values of one or more independent variables, a fitted regression model can be useful. For example, you may want to predict the sales of a product based on factors like price, advertising, and customer demographics.
- Relationship analysis: If you want to understand the relationship between a dependent variable and one or more independent variables, a fitted regression model can help. For example, you may want to understand the relationship between income and education level, or between exercise habits and health outcomes.
- Forecasting: If you want to forecast future values of a dependent variable based on historical data, a fitted regression model can be useful. For example, you may want to forecast future sales based on historical sales data and other variables like economic indicators and seasonal trends.
In general, a fitted regression model can be useful whenever there is a need to understand or predict the behavior of a dependent variable based on one or more independent variables.
Guidelines for correct usage of fit regression model
- Data collection guidelines:
- Ensure data represent the population of interest
- Collect enough data for necessary precision
- Measure variables accurately and precisely
- Record data in order collected
- Types of predictors:
- Continuous: measured and ordered, infinite values between any two values
- Categorical: finite, countable number of categories, no logical order
- Discrete: measured and ordered, countable number of values; can be treated as continuous or categorical
- Fitting models based on predictors and response variable:
- Fitted Line Plot for continuous predictor and response
- Fit General Linear Model for nested or random categorical predictors with fixed factors
- Fit Mixed Effects Model for nested or random categorical predictors with random factors
- Binary Logistic Model for response variable with two categories
- Ordinal Logistic Regression for response variable with three or more categories with natural order
- Nominal Logistic Regression for response variable with three or more categories without natural order
- Fit Poisson Model for response variable that counts occurrences
- Multicollinearity:
- Correlation among predictors should not be severe
- Use variance inflation factors (VIF) to determine severity
- Model fit:
- Model should provide good fit to data
- Use residual plots, diagnostic statistics for unusual observations, and model summary statistics to assess model fit
Alternatives: When not to use fit regression model
- To visualize the relationship between a continuous predictor and a continuous response, use a Fitted Line Plot.
- If you have categorical predictors that are nested or random, use Fit General Linear Model for all fixed factors or Fit Mixed Effects Model for random factors.
- For a response variable with two categories, use Fit Binary Logistic Model.
- For response variables with three or more categories with a natural order, such as strongly disagree to strongly agree, use Ordinal Logistic Regression.
- For response variables with three or more categories without a natural order, such as scratch, dent, and tear, use Nominal Logistic Regression.
- To analyze a response variable that counts occurrences, such as the number of defects, use Fit Poisson Model.
Example of fit regression model?
The objective of a chemist's research is to investigate the relationship between various predictors and the wrinkle resistance of cotton cloth. To achieve this, the chemist studies 32 pieces of cotton cellulose that were treated at different curing time, curing temperature, formaldehyde concentration, and catalyst ratio settings. The chemist records the durable press rating, which is an indicator of wrinkle resistance, for each cotton piece.
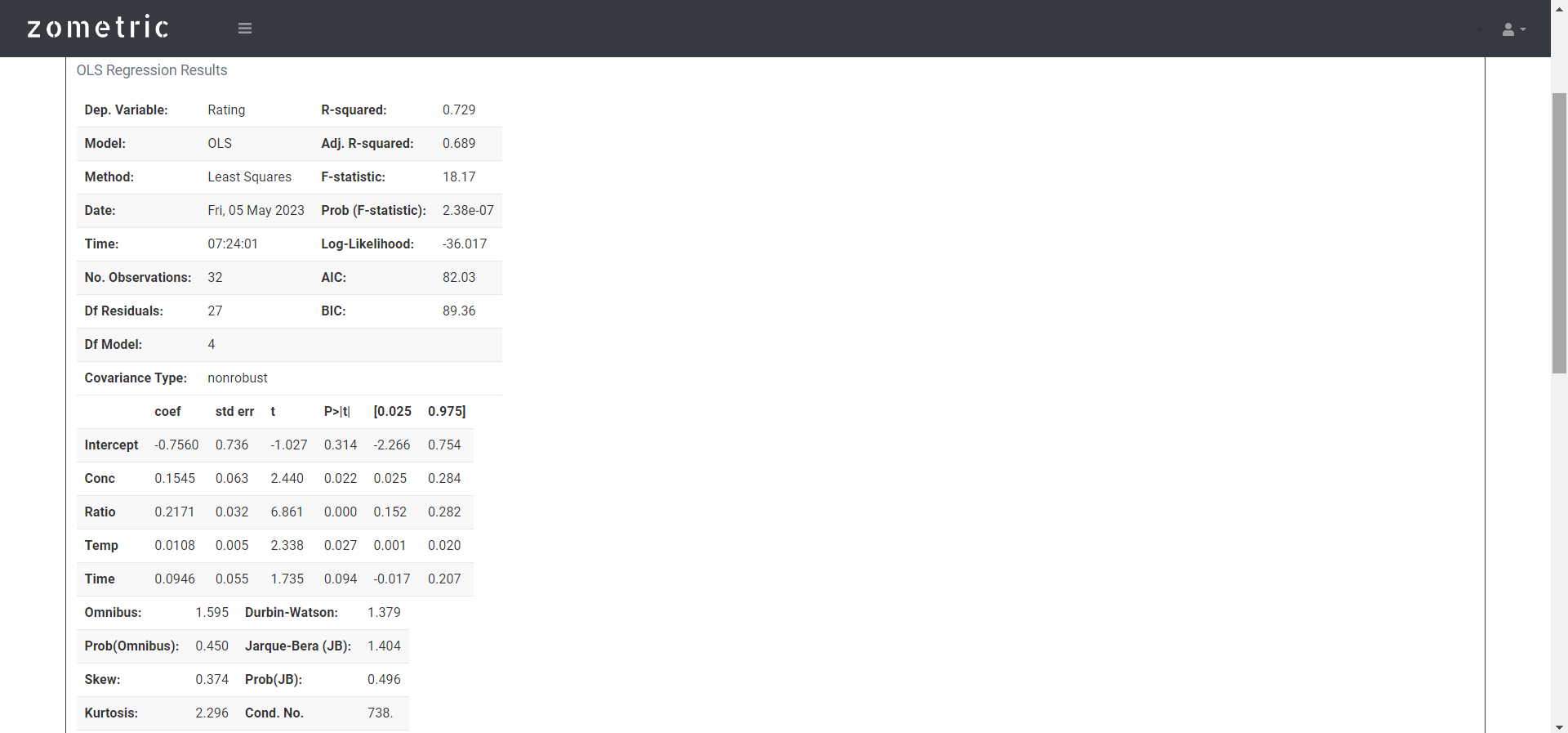
To identify the significant predictors that are related to the response, the chemist employs multiple regression analysis and eliminates those predictors that do not have a statistically significant relationship with the response. She has performed this in following steps:
- She worked all day and gathered the necessary data.
- Now, she analyzes the data with the help of https://qtools.zometric.com/
- Inside the tool, she feeds the data. Also, she chooses the desired options as follows:
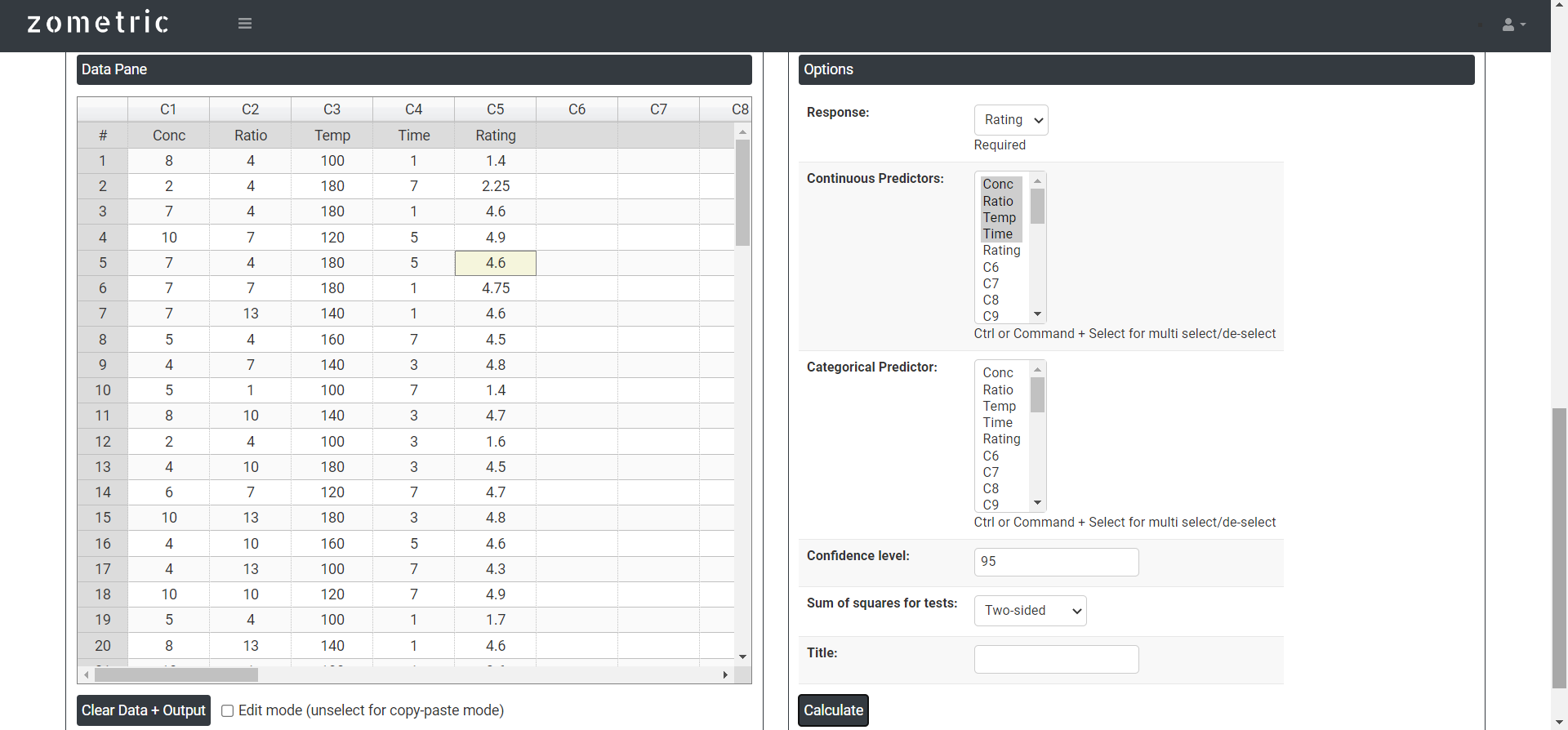
- After using the above mentioned tool, she fetches the output as follows:
How to do fit regression model
The guide is as follows:
- Login in to QTools account.
- On the home page, you can see fit regression model under Regression.
- Click on fit regression model and reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to choose the desired option.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of fit regression model, the window is separated into two parts.
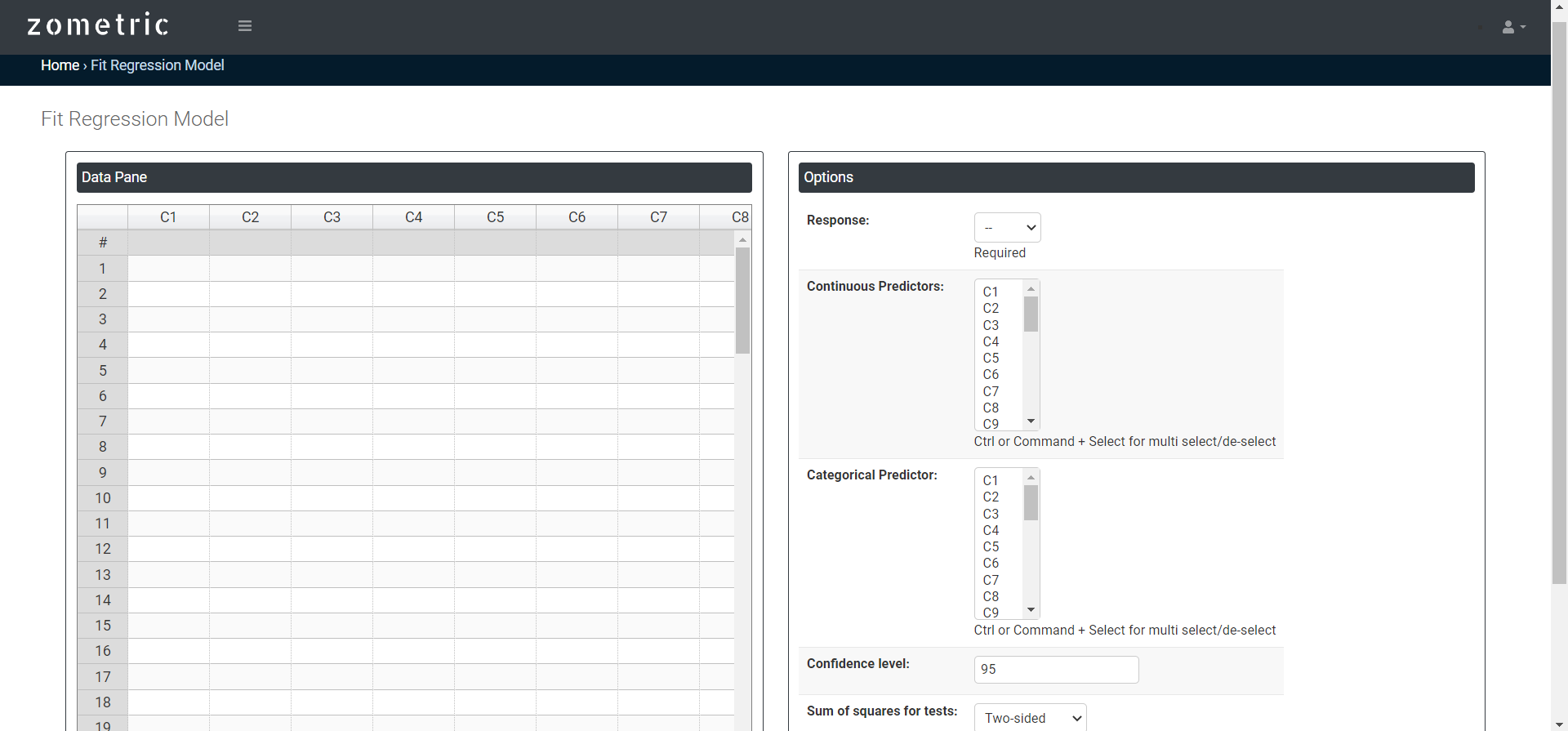
On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
On the right part, there are many options present as follows:
- Response: In a regression model, the response variable is the variable being predicted or explained by the independent variables or predictors. It is also known as the dependent variable or the target variable. The response variable is the variable that the regression model is trying to estimate or predict based on the values of the independent variables.
- Continuous Predictors: In a regression model, a continuous predictor is a variable that takes on continuous or numeric values, and is used to predict or explain the variation in the response variable. Continuous predictors can take on any value within a certain range or interval, and can have decimal places or fractions.
- Categorical Predictors: In regression analysis, categorical predictors are variables that take on a limited number of discrete values, often referred to as categories or levels. These variables are also known as qualitative or nominal variables, as opposed to quantitative or numerical variables.
- Confidence level: In regression analysis, the confidence level is a measure of the precision and accuracy of the estimated coefficients of the regression model. Specifically, the confidence level refers to the probability that the true population value of a coefficient falls within a certain range of values, given the sample data used to estimate the coefficient. The confidence level is typically expressed as a percentage, and a common value is 95%. This means that if the same regression model were estimated repeatedly using different samples of data, 95% of the time the estimated coefficient would fall within the confidence interval for that coefficient.
- Sum of squares for tests:
- Two sided: The two-sided sum of squares (SS) is a statistical measure used in hypothesis testing for the regression model. It measures the deviation between the observed data and the predicted values based on the regression model. In a regression analysis, the two-sided SS is calculated as the sum of the squared differences between the observed values and the predicted values, for both the explained and unexplained variation in the data. It is called "two-sided" because it considers both positive and negative deviations between the observed and predicted values.
- Lower bound: The lower bound sum of squares for tests in a fitted regression model is typically used in hypothesis testing to determine whether a particular predictor variable has a significant effect on the outcome variable. It is also known as the residual sum of squares (RSS), or the sum of squared errors (SSE).
- Upper bound: The upper bound for the sum of squares in a regression model is determined by the total sum of squares (TSS), which is the sum of the squared differences between the dependent variable and its mean. The sum of squares due to error (SSE) represents the variation in the dependent variable that is not explained by the model. The upper bound for the sum of squares for a particular test can be calculated by dividing the sum of squares due to regression (SSR) by the degrees of freedom (df) for the regression model. This value is known as the mean sum of squares (MSR).