What is One sample proportion test?
One sample proportion test is a statistical method used to determine whether a proportion of a single population differs significantly from a hypothesized value. It is often used in research studies to test the significance of a single proportion or the proportion of a certain characteristic in a population.
The test involves collecting a sample from the population of interest and calculating the sample proportion, which is then compared to the hypothesized value using a statistical test such as the z-test or chi-square test. The null hypothesis is that the sample proportion is equal to the hypothesized value, and the alternative hypothesis is that it is not.
When to use One sample proportion test?
One sample proportion test is used when we want to determine whether the proportion of a certain characteristic in a single population differs significantly from a hypothesized value.
Here are some scenarios where one might use a one sample proportion test:
- A marketing company wants to determine whether the proportion of consumers who prefer their brand over their competitor's brand is higher than a certain value, such as 50%.
- A public health agency wants to determine whether the proportion of people in a certain population who have received a certain vaccine is lower than a certain value, such as 80%.
- An educational institution wants to determine whether the proportion of students who pass a certain exam is higher than a certain value, such as 70%.
In each of these scenarios, a one sample proportion test would be used to determine whether the observed proportion is significantly different from the hypothesized value. This can help in making decisions or drawing conclusions about the population of interest.
Guidelines for correct usage of One sample proportion test
- Random sampling should be used to make inferences about the population.
- Only data with two categories should be used for hypothesis testing.
- Each observation should be independent from all other observations.
- Adequate sample size should be determined to ensure precision of estimates, narrow confidence intervals, and adequate protection against errors.
Alternatives: When not to use One sample proportion test
- When dealing with count data, such as the number of defects in a product, you should use the 1-Sample Poisson Rate test.
Example of One sample proportion test?
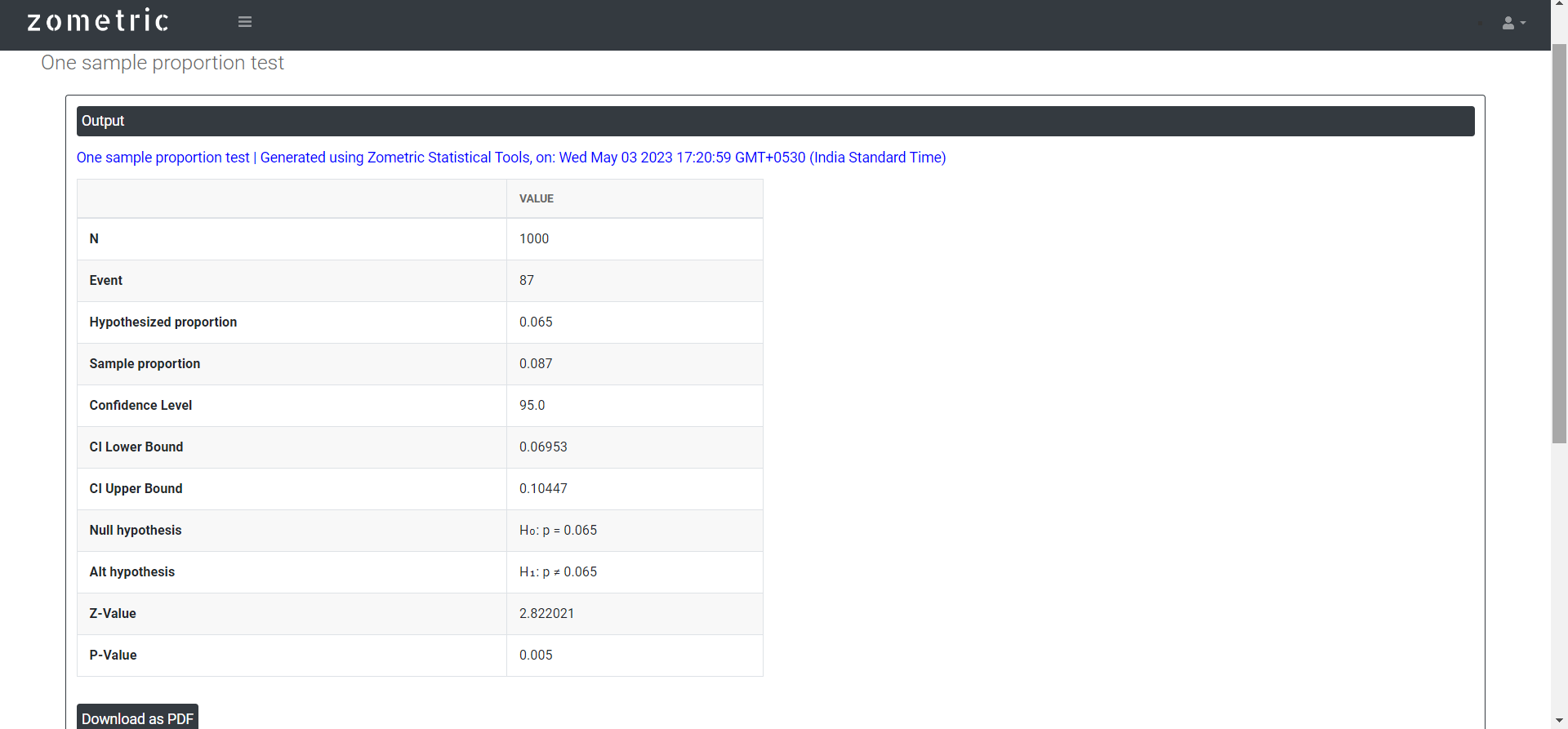
A marketing analyst wants to determine whether mailed advertisements for a new product result in a response rate different from the national average. A random sample of 1000 households is chosen to receive advertisements. Of the 1000 households sampled, 87 make a purchase after receiving the advertisement. The analyst performs a One sample proportion test to determine whether the proportion of households that made a purchase is different from the national average of 6.5%. She has performed this in following steps:
- She analyzes the data with the help of https://qtools.zometric.com/
- Inside the tool, she feeds the data. She puts number of events as 87, number of trials as 1000, hypothesized proportion as 0.065 and confidence level as 95.
- After using the above mentioned tool, she fetches the output as follows:
How to do One sample proportion test
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/
- On the home page, you can see One sample proportion test under Hypothesis Tests.
- Click on One sample proportion test and reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to put the values of number of events, number of trials, hypothesized proportion and confidence level.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of One sample proportion test, the window has only left part.
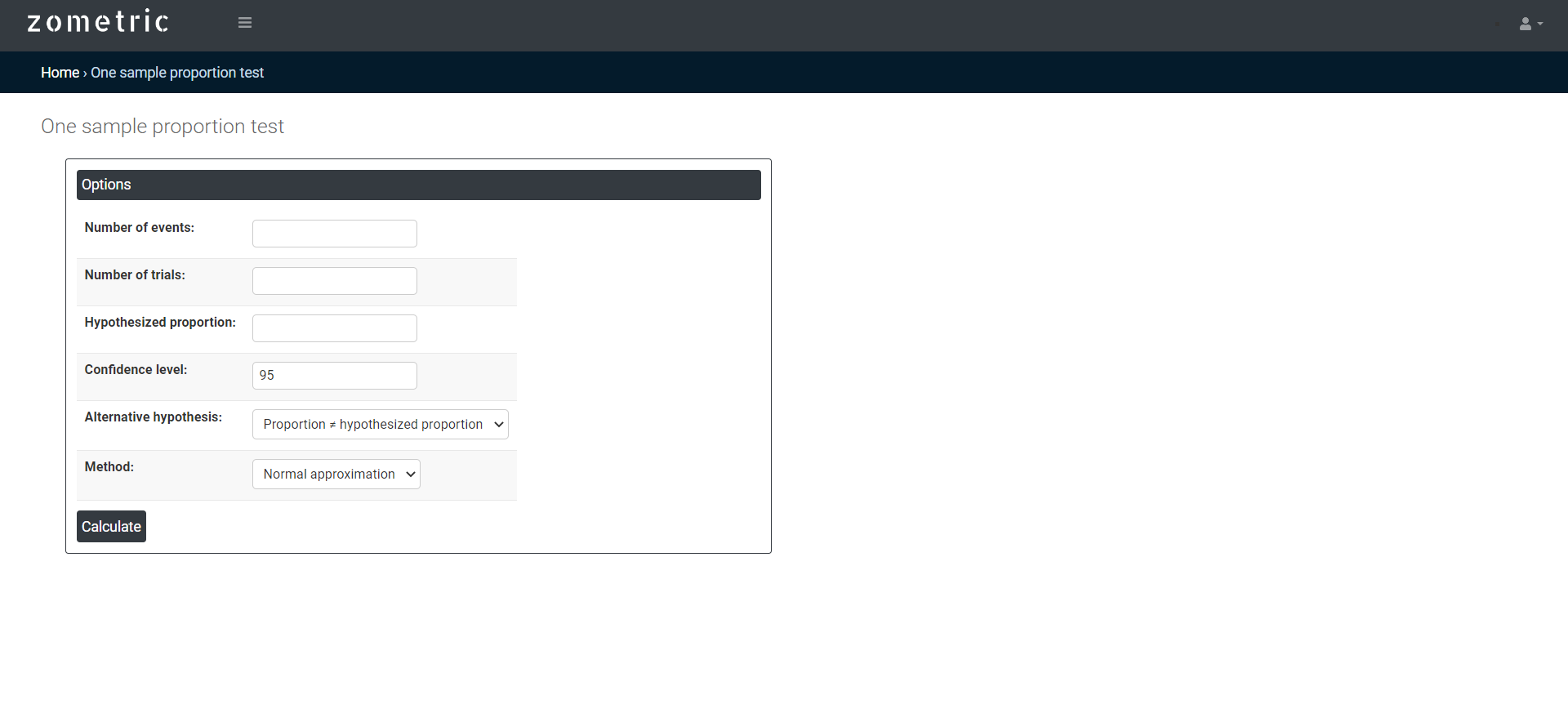
In this left part, there are many options present as follows:
- Number of events: In a one sample proportion test, the number of events refers to the number of occurrences of the event of interest in the sample being analyzed.
- Number of trials: In a one sample proportion test, the number of trials refers to the number of independent, identical trials or observations made on the sample being analyzed.
- Hypothesized proportion: In a one sample proportion test, the hypothesized proportion (also called the null hypothesis proportion) is the proportion that is assumed to be true for the population being tested
- Confidence level: In hypothesis testing, the confidence level represents the degree of certainty or level of confidence that we have in our statistical analysis. It is a probability value that indicates the likelihood that the true population parameter falls within the specified range of values. Typically, the confidence level is expressed as a percentage and is denoted by (1 - α), where α is the level of significance or the probability of rejecting a true null hypothesis. For example, if we have a confidence level of 95%, then we are saying that we are 95% confident that the true population parameter lies within our interval estimate, and there is a 5% chance of making a type I error (rejecting a true null hypothesis). In practical terms, a higher confidence level means that we are more confident in our statistical analysis and results. However, increasing the confidence level also increases the width of the confidence interval, making it more difficult to detect small effects. Therefore, the choice of the confidence level depends on the context of the study and the goals of the researcher.
- Alternative hypothesis: In hypothesis testing, the alternative hypothesis (also called the research hypothesis) is a statement that represents a different conclusion than the null hypothesis. The null hypothesis typically represents the status quo or the assumption that there is no significant difference or relationship between two or more groups or variables. The alternative hypothesis is the statement that is being tested, and it proposes that there is a significant difference or relationship between the groups or variables being studied.
- Normal approximation method: The normal approximation method is a statistical method used in one sample proportion tests to approximate the sampling distribution of the sample proportion as a normal distribution. This method is used when the sample size is sufficiently large (typically, when the sample size n is greater than or equal to 30) and the proportion of successes in the sample is not too close to 0 or 1.