Non Normal Process capability

What is Non Normal Process Capability?

When to use Non Normal Process Capability?

Nonnormal process capability should be used when the data you're analyzing doesn't follow a normal distribution, meaning it doesn't have the typical bell-shaped curve that is symmetrical and centered around the mean. Here are some situations where you'd use nonnormal process capability:

1. Skewed Data: If your data is skewed to the left or right, meaning most values are clustered on one side, a nonnormal process capability analysis is more appropriate.
2. Presence of Outliers: If your data has extreme values that don't fit the overall pattern, they can distort a normal distribution. Nonnormal analysis can handle these outliers better.
3. Non-Symmetrical Distributions: When the data shows a pattern that isn't symmetric (e.g., log-normal or exponential distributions), nonnormal process capability helps provide a more accurate assessment.
4. Multiple Peaks: If your data has more than one peak (bimodal or multimodal distribution), it doesn't follow a normal distribution and should be analyzed with nonnormal methods.
5. Process Characteristics: Some processes naturally produce nonnormal data due to the nature of the process or the product. For example, wear and tear over time, batch processes, or processes with inherent limits might produce nonnormal data.
6. Non-Linear Relationships: When the relationship between variables isn't linear, the data might not be normally distributed, making nonnormal process capability a better choice.

Guidelines for correct usage of Non Normal Process Capability

• Use continuous data for the analysis; if dealing with attribute data, apply Binomial or Poisson Capability Analysis instead.
• Collect at least 100 data points to ensure reliable process capability estimates and accurate representation of process variation.
• Ensure the process is stable and in control before conducting capability analysis, using tools like Xbar-S Chart or Nonnormal Capability Sixpack if necessary.
• The data must closely follow the selected nonnormal distribution; use Individual Distribution Identification to find the best fit for accurate capability estimates.

Alternatives: When not to use Non Normal Process Capability

• If you’re unsure which nonnormal distribution fits your data, use Individual Distribution Identification before the analysis.
• For checking process control and suitability for a specific nonnormal distribution, use Nonnormal Capability Sixpack first.
• To estimate within-subgroup variation and potential capability along with overall capability, use Normal Capability Analysis to transform nonnormal data and assess it based on a normal distribution.

Example of Non Normal Process Capability?

An automotive component manufacturer is assessing whether a drilling machine can meet the specifications for a critical component. The component must fall within a range: Lower Specification Limit (LSL) of 22.15 and Upper Specification Limit (USL) of 22.35. To evaluate this, the engineer takes 125 samples from the machine and performs the following steps:

1. Gathered the necessary data.

2.  Now analyses the data with the help of  https://qtools.zometric.com/ or https://intelliqs.zometric.com/.
3.  To find Non Normal Process Capability choose https://intelliqs.zometric.com/> Statistical module> Process Capability>Non Normal Process Capability.
4.  Inside the tool, feeds the data along with other inputs as follows:

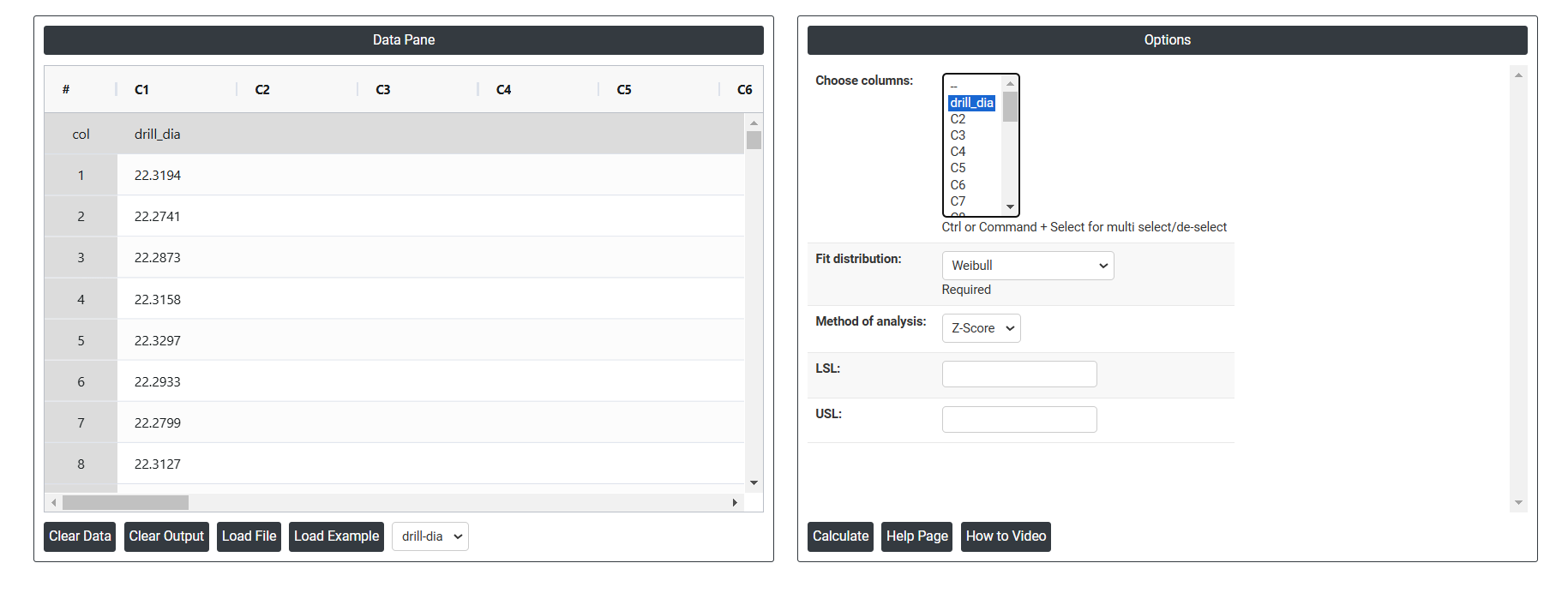
5. After using the above mentioned tool, fetches the output as follows:

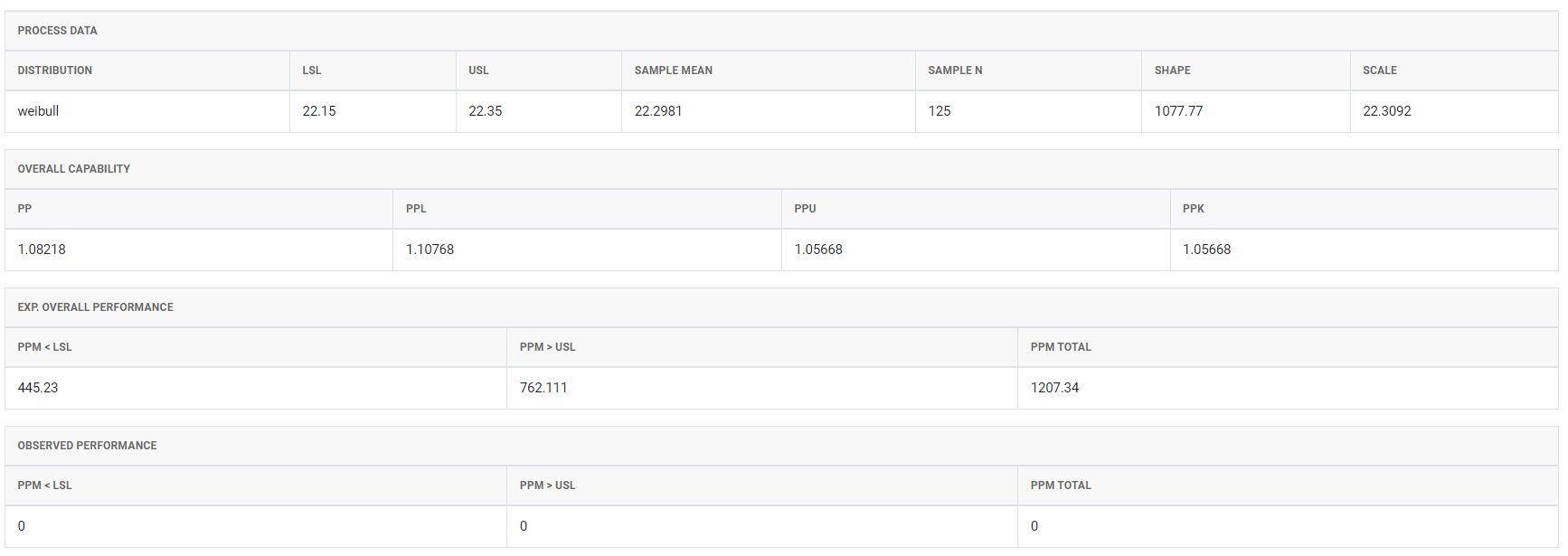
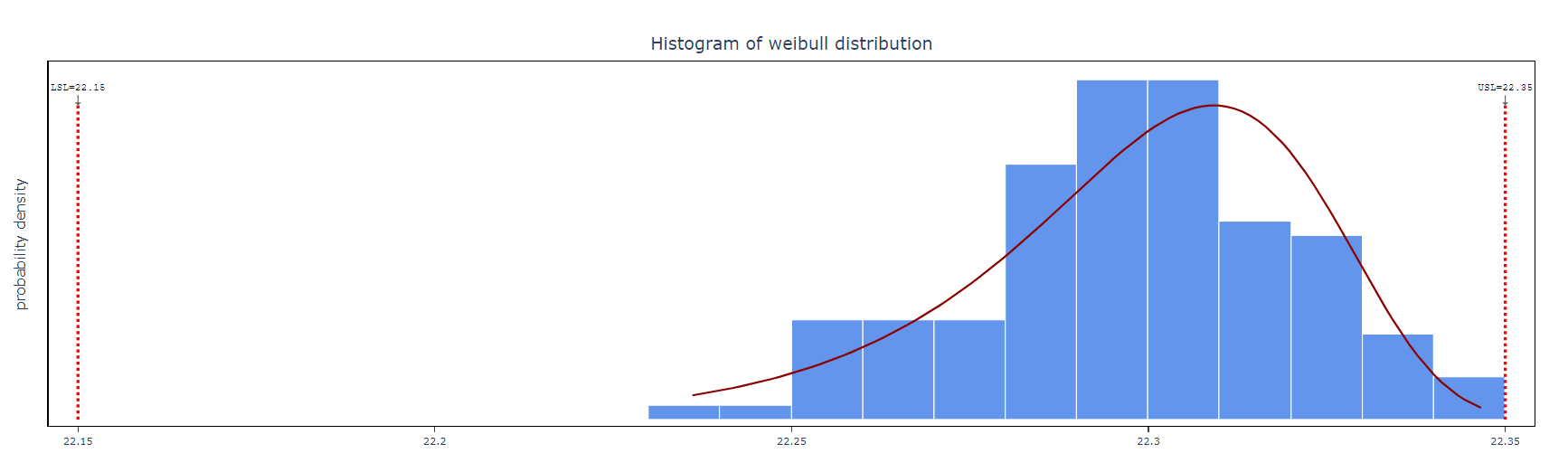
How to do Non Normal Process Capability

The guide is as follows:

1. Login in to QTools account with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/
2. On the home page, choose Statistical Tool> Process Capability >Non Normal Process Capability.
3. Click on Non Normal Process Capability and reach the dashboard.
4. Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
5. Next, you need to put the values of confidence level and hypothesized mean.
6. Finally, click on calculate at the bottom of the page and you will get desired results.

On the dashboard of Non Normal Process Capability, the window is separated into two parts.

On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.

Load example: Sample data will be loaded.

Load File: It is used to directly load the excel data.

On the right part, there are many options present as follows:

• Fit Distribution:
  • Weibull distribution: The Weibull distribution is a flexible statistical model used in engineering, medical research, finance, and climatology, particularly for analyzing time-to-failure data and handling skewed process data. It is defined by three parameters: shape, scale, and threshold. The 3-parameter Weibull distribution includes all three, while the 2-parameter version, which excludes the threshold, is used for positive values only. The shape parameter affects the distribution’s skewness, the scale parameter indicates the point where 63.2% of the population is expected to fail, and the threshold parameter shifts the distribution along the time axis. This distribution is crucial for predicting failures, estimating life cycles, and understanding complex data patterns. Its versatility extends to quality control and risk management as well.
  • Exponential: The exponential distribution is a continuous probability distribution that is frequently used in process capability analysis when dealing with non-normal data, particularly in scenarios such as time-to-failure data, where the likelihood of failure decreases over time, and inter-arrival times for events in a Poisson process, where events happen continuously and independently at a constant average rate. This distribution is ideal for modeling the time until a specific event occurs, with its memoryless property making it well-suited for situations where the past does not influence the future, allowing for accurate analysis of skewed data that does not follow a normal distribution.
  • Logistic: The logistic distribution plays a significant role in non-normal process capability analysis , especially when the data is symmetrical but not normally distributed. The logistic distribution is similar in shape to the normal distribution but has heavier tails, meaning it gives more probability to extreme values. This characteristic makes it useful in certain process capability analyses where data tends to have outliers or a greater spread than what the normal distribution would accommodate.
  • Loglogistic: It is particularly useful when the data is symmetric like the normal distribution but has heavier tails, meaning it allows for more extreme values. This makes it suitable for processes where extreme deviations from the mean are more likely than what a normal distribution would predict.
  • Largest Extreme Value: The Largest Extreme Value distribution is essential in non-normal process capability analysis when dealing with data focused on maximum values or right-skewed distributions. It ensures that extreme values are accurately modeled, leading to more reliable capability assessments and better-informed decisions about process performance and risks.
  • Smallest Extreme Value: The smallest extreme value (SEV) distribution plays a critical role in non-normal process capability analysis, especially when the data is skewed and does not fit the normal distribution. The SEV distribution is particularly useful for modeling the minimum values in a dataset, such as the smallest time to failure or the weakest link in a chain of events.
  • 2-Parameter Exponential: The 2-parameter exponential distribution is defined by a scale parameter (λ) and a threshold parameter (θ). The threshold parameter shifts the distribution by θ units to the right, indicating a minimum waiting time before events can occur. The scale parameter controls the rate at which events occur after the threshold.
  • 3- Parameter Weibull: The 3-parameter Weibull distribution is defined by a shape parameter (β), a scale parameter (η), and a threshold parameter (γ). The shape parameter (β) determines the failure rate behavior, the scale parameter (η) indicates the characteristic life, and the threshold parameter (γ) shifts the distribution, representing the minimum time before failures start. This distribution is used for modeling life data with an initial waiting period before events can occur, adding flexibility for more accurate data fitting.
  • Gamma: The gamma distribution is a continuous probability distribution characterized by a shape parameter (k or α) and a scale parameter (θ). It is primarily used to model the waiting time until a specified number of events occur, making it ideal for processes involving accumulated times or skewed data.
  • Lognormal: The lognormal distribution is a continuous probability distribution where the logarithm of the random variable is normally distributed. It is characterized by being positively skewed and is defined by the mean (μ) and standard deviation (σ) of the underlying normal distribution. Commonly used in finance, life sciences, and reliability analysis, it models data that must remain positive and exhibit multiplicative growth or right-skewed behavior.
• LSL: This is the minimum acceptable value for a process measurement. Any value below this limit indicates that the product or process does not meet quality standards and is considered defective.
• USL: This is the maximum acceptable value for a process measurement. Any value above this limit also indicates that the product or process is out of specification and does not meet quality requirements.
• Method of Analysis:
• Z-Score: The Z-score method calculates how many standard deviations each data point is from the mean, helping assess process capability against specification limits. It is particularly useful for nonnormal data and provides capability indices like Cp and Cpk, which indicate how well a process fits within those limits. The method helps identify performance issues, enabling data-driven decisions for quality improvement.

       Use this method when:

• The data do not follow a normal distribution, which is common in many real-world processes.
• You need a more flexible approach that can accommodate various distributions (e.g., exponential, lognormal).
• You want to calculate process capability indices (Cp, Cpk) that are standardized in terms of how many standard deviations the process mean is from the specification limits.

       Advantages:

• The Z-score method provides a clearer understanding of process performance relative to specification limits by expressing capability in standard deviations.
• It allows for better comparisons between different processes or characteristics, even when the data are nonnormal.
• ISO: The ISO method in Minitab, based on the ISO 13528 standard, provides a structured approach to process capability analysis by using multiple methods for calculating z-scores, such as z-prime and zeta scores. It defines specific thresholds for interpreting z-scores: values greater than 3 indicate significant deviations (action signals) requiring immediate attention, while values greater than 2 serve as warnings of potential issues. This method emphasizes standardization and is particularly useful in regulated industries, ensuring consistent quality measurement and effective statistical process control.
• Download as Excel: This will display the result in an Excel format, which can be easily edited and reloaded for calculations using the load file option.