What is one way ANOVA?
One way ANOVA (Analysis of Variance) is a statistical test used to compare the means of three or more groups that are independent of each other. It is called "one way" because it considers only one factor or independent variable that divides the subjects or observations into groups.
The one way ANOVA tests whether the means of these groups are significantly different from each other. Specifically, it measures the variation between the means of the groups, compared to the variation within each group.
When to use one way ANOVA?
One way ANOVA (Analysis of Variance) is used to determine whether there are any statistically significant differences between the means of two or more independent groups. This test is appropriate when you have a continuous dependent variable and a categorical independent variable with three or more levels.
Some common examples of when one way ANOVA might be used include:
- Comparing the average scores of students who took different types of classes (e.g., online vs. in-person vs. hybrid).
- Analyzing the effectiveness of three or more different drugs in treating a disease.
- Comparing the average salaries of employees in three or more different departments within a company.
Overall, one way ANOVA is a useful statistical test for comparing the means of multiple groups and can provide valuable insights for research and decision-making.
Guidelines for correct usage of one way ANOVA
Guidelines for data collection, analysis, and result interpretation:
- Include only one categorical variable that is a fixed factor
- Use Fit General Linear Model or Fit Mixed Effects Model for two or more fixed categorical factors
- Use Fitted Line Plot to plot relationship between one continuous predictor and response
- Response variable should be continuous
- Use Fit Binary Logistic Model for two categories
- Use Ordinal Logistic Regression for three or more categories with natural order
- Use Nominal Logistic Regression for three or more categories without natural order
- Use Fit Poisson Model if response variable counts occurrences
- Sample data should be from a normal population or have a sample size >15-20
- Sample size guidelines depend on number of groups: 2-9 groups need at least 15/sample, 10-12 groups need at least 20/sample
- Use Kruskal-Wallis Test if not confident that data follow a normal distribution and sample size guidelines not met
- Ensure each observation is independent from all other observations
- Collect data using best practices: represent population of interest, collect enough data for necessary precision, measure variables accurately and record in order collected
- Model should provide a good fit to the data, use residual plots, diagnostic statistics, and model summary statistics to check fit.
Alternatives: When not to use one way ANOVA
- In case you have multiple categorical factors that are fixed, use the Fit General Linear Model if all of them are fixed factors.
- If there are random factors, use the Fit Mixed Effects Model instead.
- If you wish to visualize the connection between a continuous predictor and response, use the Fitted Line Plot.
- When you have more than one predictor, use the Fit Regression Model.
Example of one way ANOVA?
The chemical engineer intends to evaluate the hardness of four different paint blends by applying six samples of each blend to a metal piece, curing them, and measuring their hardness. To test for the similarity of means and to examine the variations between pairs of means, the analyst employs one-way ANOVA with multiple comparisons. She has performed this in following steps:
- She worked all day and gathered the necessary data.
- Now, she analyzes the data with the help of https://qtools.zometric.com/
- Inside the tool, she feeds the data. Also, she puts 95 as the confidence level.
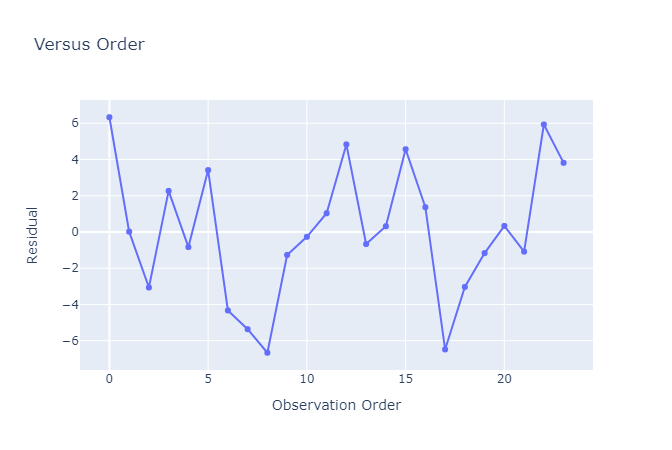
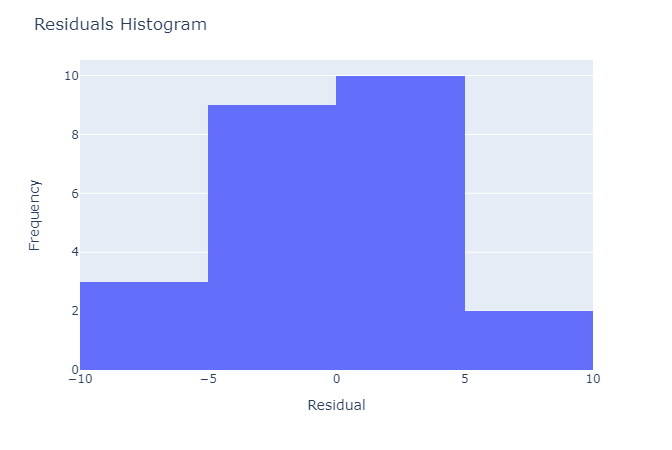
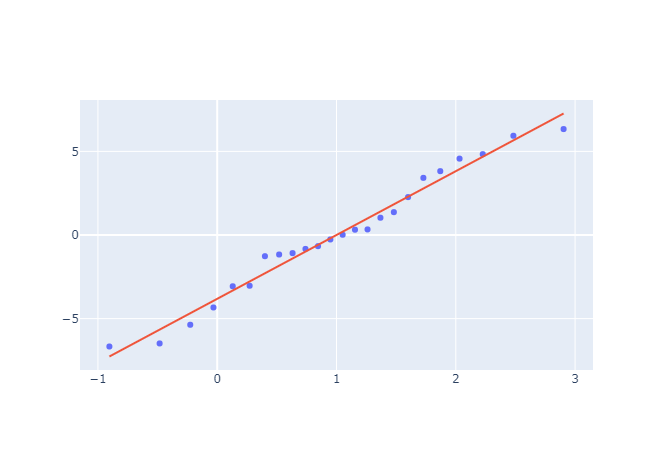
- After using the above mentioned tool, she fetches the output as follows:
How to do one way ANOVA
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/
- On the home page, you can see one way ANOVA under ANOVA.
- Click on one way ANOVA and reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to put the value of confidence level.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of one way ANOVA, the window is separated into two parts.
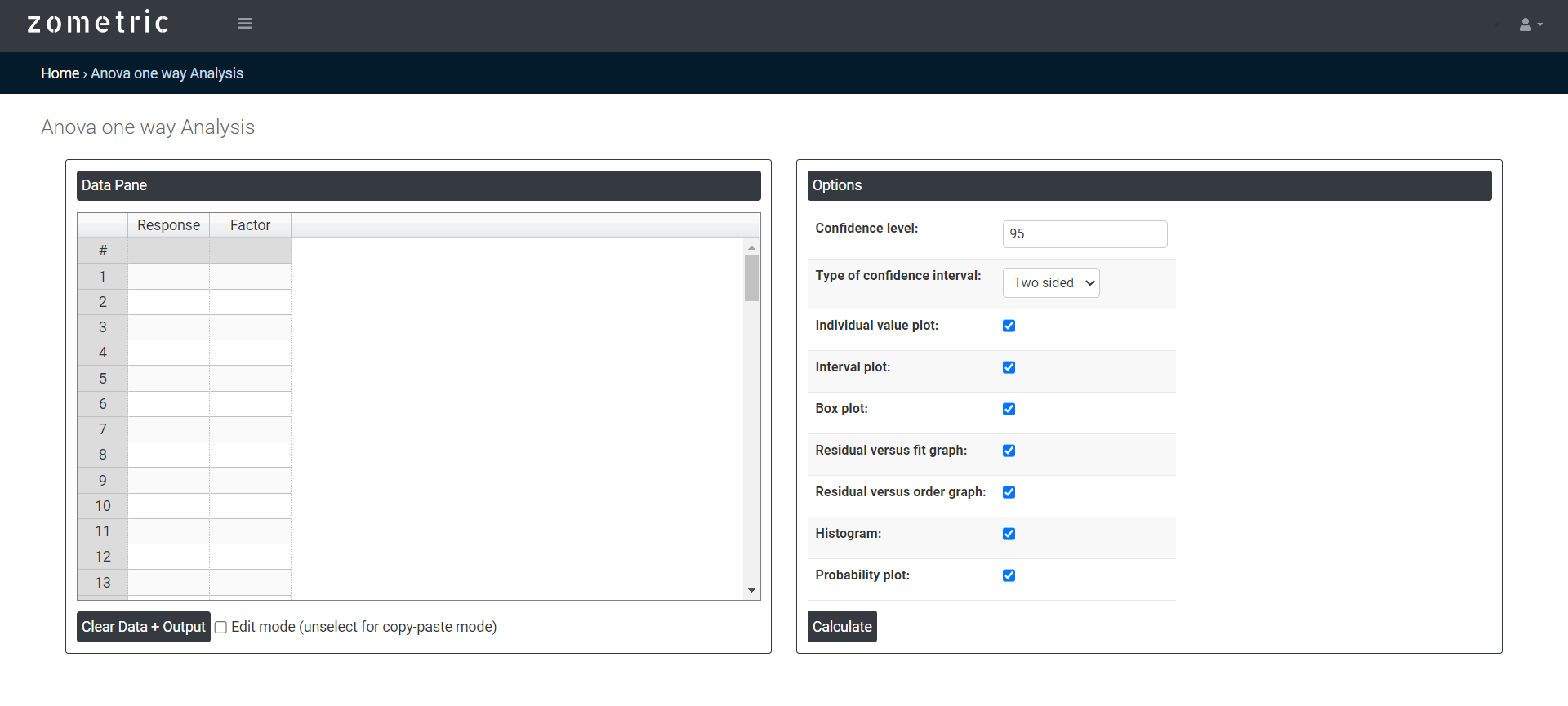
On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
On the right part, there are many options present as follows:
- Confidence level: In one-way ANOVA (analysis of variance), the confidence level refers to the degree of certainty that a statistical analysis provides. It is the probability that the difference observed between the groups in the study is not due to random chance. The confidence level is typically expressed as a percentage, and it represents the degree of certainty that the results obtained from the sample data will be representative of the larger population. A common confidence level used in statistical analysis is 95%.
- Two sided confidence level: In one-way ANOVA, a two-sided confidence level refers to the interval estimate of the difference in means between groups in both directions, above and below the sample mean. It provides a range of values that contains the true population mean with a certain degree of confidence.
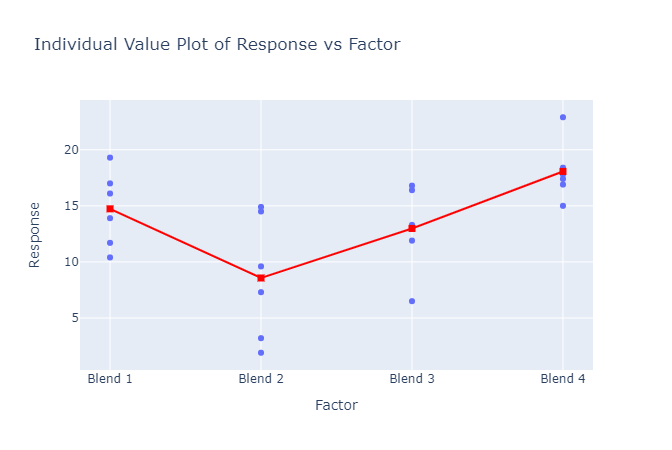
- Individual value plot: An individual value plot, also known as a strip plot or dot plot, is a graphical representation of the data used in one-way ANOVA. In one-way ANOVA, we compare the means of three or more groups to determine if there is a significant difference between them. An individual value plot displays the data points for each group as dots or strips along the horizontal axis, with the vertical axis representing the variable being measured. The dots or strips are positioned according to their corresponding group mean.
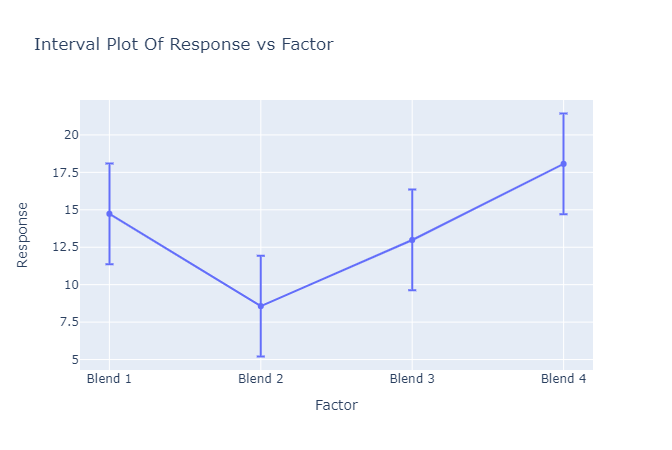
- Interval plot: An interval plot, also known as a mean plot or a confidence interval plot, is a graphical representation of the means and confidence intervals for each group used in one-way ANOVA. In one-way ANOVA, we compare the means of three or more groups to determine if there is a significant difference between them. An interval plot displays the mean value for each group as a dot or symbol on the horizontal axis, with the vertical axis representing the variable being measured. Additionally, a horizontal line or a vertical bar is drawn above and below each mean to represent the confidence interval around that mean. The length of the line or bar represents the width of the confidence interval.
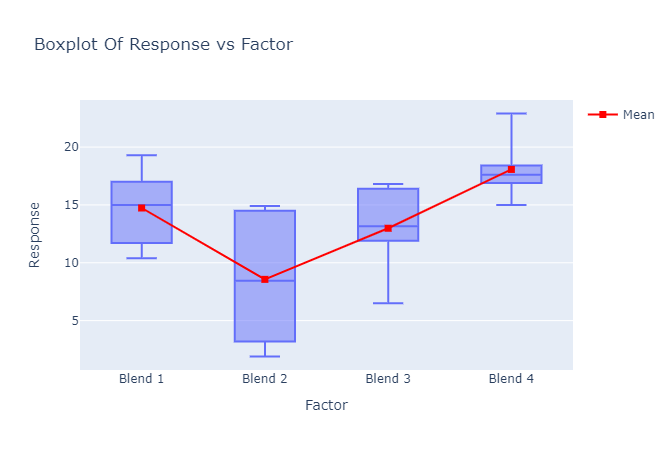
- Box plot: A box plot is a graphical representation of data that shows the distribution of a variable within different groups in a one-way ANOVA analysis. In a one-way ANOVA, we compare the means of a continuous variable across different levels of a categorical variable. The box plot displays the distribution of the continuous variable for each group, including the median, interquartile range (IQR), and any outliers.
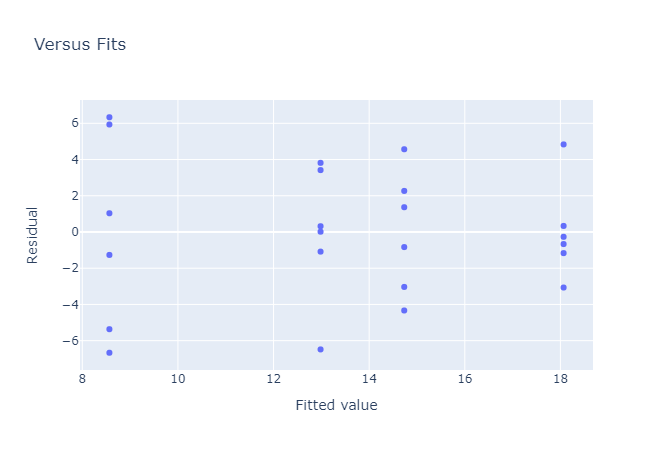
- Residual versus fit graph: A residual versus fit graph, also known as a residual plot, is a graphical tool used in one-way ANOVA to assess the goodness of fit of the model. The plot displays the residuals, which are the differences between the observed values and the predicted values, on the y-axis and the predicted values on the x-axis.
- Residual versus order graph: In one-way ANOVA, a residual versus order graph is a graphical tool used to assess the assumption of equal variance of the residuals across different levels of the factor or independent variable. In this graph, the residuals (i.e., the differences between the observed values and the predicted values) are plotted against the order of the observations, which can be simply the sequence of the data points or the level of the factor. The residuals should be randomly scattered around zero and should not show any systematic pattern or trend as the order or level of the factor changes.
- Histogram: A histogram is a graphical representation of the distribution of a set of data. In the context of one-way ANOVA (analysis of variance), a histogram is often used to visualize the distribution of the dependent variable (i.e., the variable being analyzed) for each group in the study.
- Probability plot: A probability plot, also known as a quantile-quantile (Q-Q) plot, is a graphical tool that is often used in statistical analysis to assess whether a set of data follows a particular distribution. In the context of one-way ANOVA (analysis of variance), a probability plot can be used to assess whether the assumption of normality holds for the residuals (the differences between the observed data and the model predictions) of the ANOVA model.