Try Statistical Software for Free
What is Two Sample t test?
A two-sample t-test is a statistical method used to determine if there is a significant difference between the means of two independent groups. This test is applicable when the population variances are unknown and the data for each group are assumed to be normally distributed. The two-sample t-test can be conducted as either an independent (unpaired) t-test or a paired t-test, depending on the nature of the samples.
Using a one-sample t-test, you can:
- Assess if the sample mean differs from a specified hypothesized mean.
- Estimate a range of values (confidence interval) that is likely to include the population mean.
When to use Two Sample t test?
This test is commonly used in scientific research and data analysis to determine if there is a significant difference between the means of two groups.
- Key Conditions:
Independent Samples
Normal Distribution
Unknown Population Variances
Here are some scenarios when a two sample t test may be appropriate:
- Medical research: A drug is tested to see if it has an effect on a particular condition, and the researchers compare the mean response of a treatment group to that of a control group.
- Market research: A company wants to know if there is a significant difference in the amount of money spent by two different demographic groups on a new product.
- Educational research: A new teaching method is introduced, and the mean test scores of students in a treatment group are compared to the mean test scores of a control group.
Guidelines for correct usage of Two sample t test
- Data must be continuous and each observation should be independent.
- Sample data should be selected randomly.
- If data contain counts, use 2-Sample Poisson Rate.
- If data classify each observation into one of two categories, use 2 Proportions.
- Sample data should not be severely skewed.
- Each sample size should be greater than 15.
- Determine an appropriate sample size to ensure precision and narrow confidence intervals.
Alternatives: When not to use Two sample t test
- If your data is paired or dependent, for instance, if you have measurements of a bearing taken with two different calipers, then use Paired t.
Example of Two sample t test?
A consultant wants to compare the effect of two fertilizer formulations on the rate of growth of plants. He collects data from two sets of plants that were planted at the same time but treated with different fertilizer formulations. He uses a two-sample t-test to determine if there is a significant difference in the growth rates between the two groups of plants. The following steps:
- Gathered the necessary data.
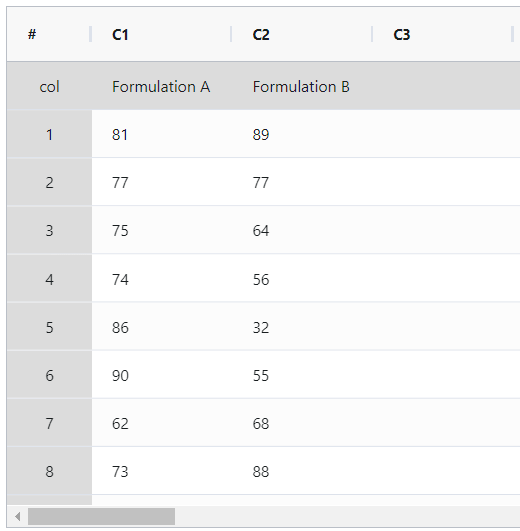
- Now analyses the data with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/.
- To find Two sample t-test choose https://intelliqs.zometric.com/> Statistical module> Graphical analysis> Two sample t-test.
- Inside the tool, feeds the data along with other inputs as follows:
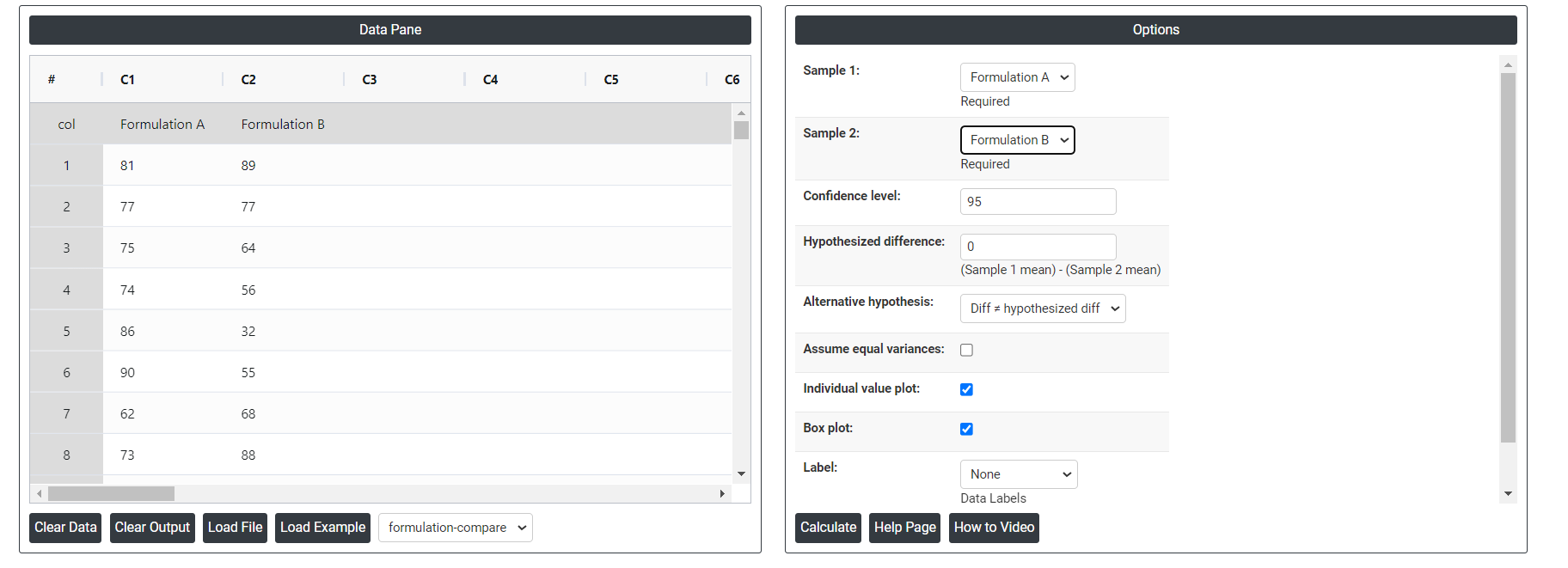
5. After using the above mentioned tool, fetches the output as follows:
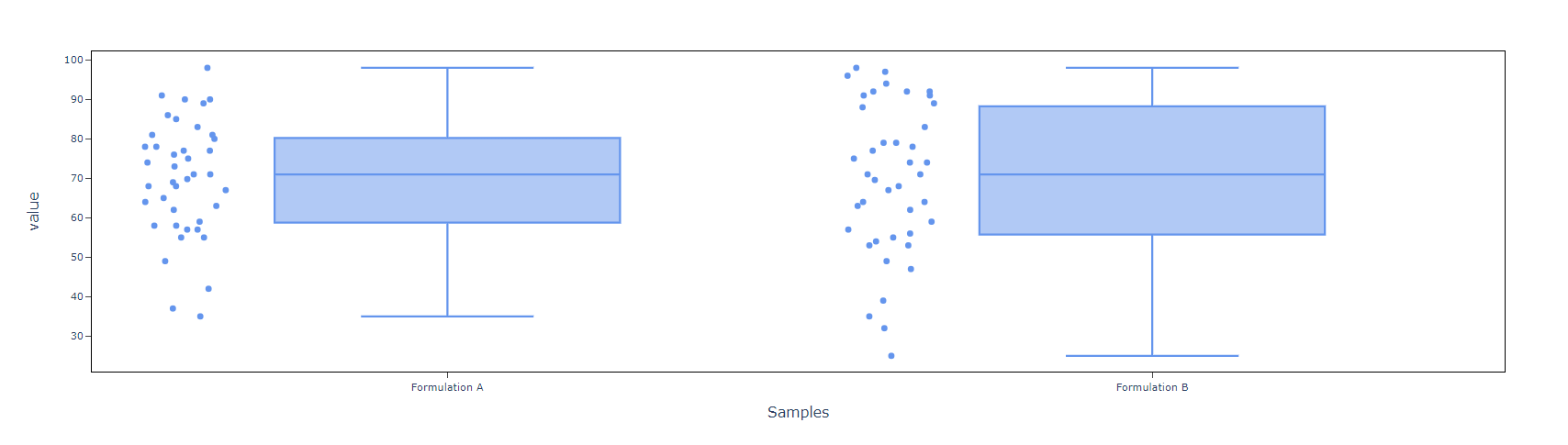
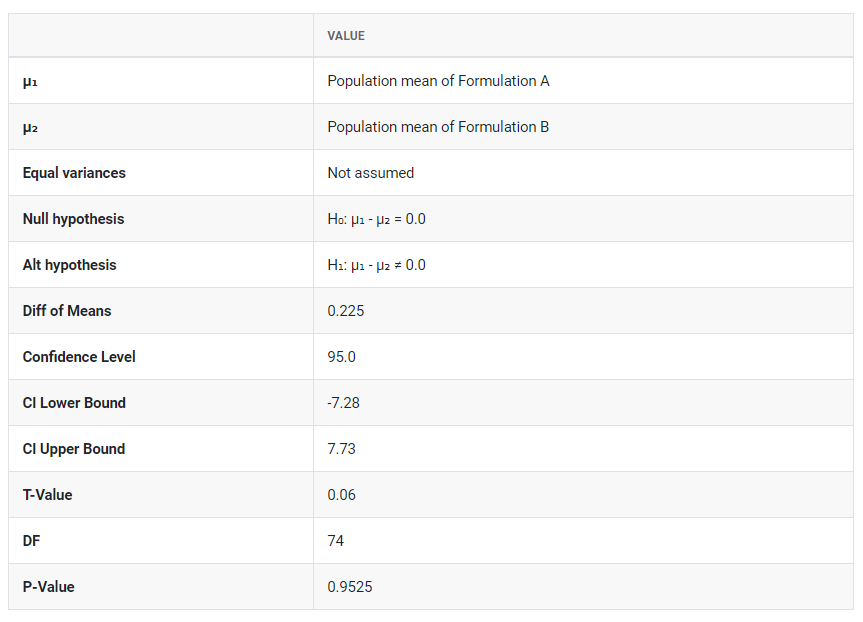
How to do Two sample t test
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/
- On the home page, choose Statistical Tool> Graphical analysis >Two sample t test
- Click on Two sample t test and reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to put the values of confidence level and hypothesized difference.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of Two sample t test, the window is separated into two parts.
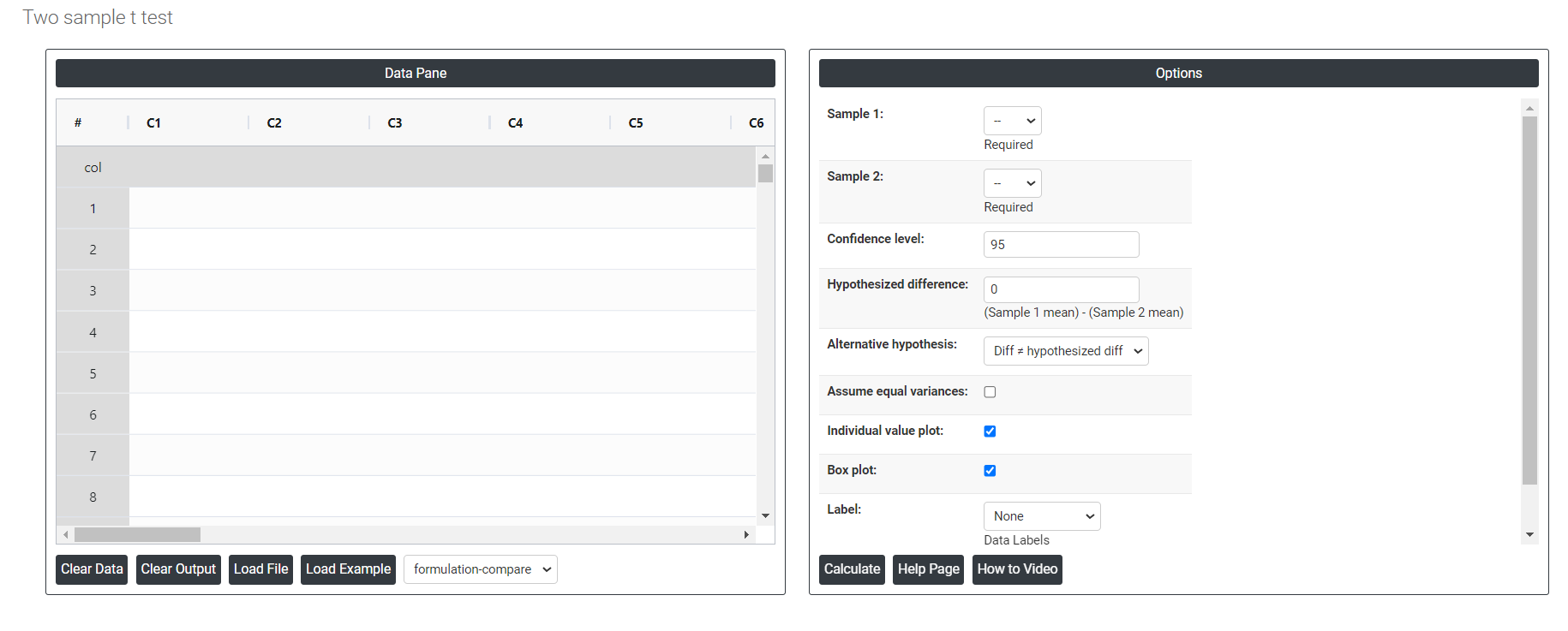
On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
Load example: Sample data will be loaded.
Load File: It is used to directly load the excel data.
On the right part, there are many options present as follows:
- Confidence level: In hypothesis testing, the confidence level represents the degree of certainty or level of confidence that we have in our statistical analysis. It is a probability value that indicates the likelihood that the true population parameter falls within the specified range of values.Typically, the confidence level is expressed as a percentage and is denoted by (1 - α), where α is the level of significance or the probability of rejecting a true null hypothesis. For example, if we have a confidence level of 95%, then we are saying that we are 95% confident that the true population parameter lies within our interval estimate, and there is a 5% chance of making a type I error (rejecting a true null hypothesis).In practical terms, a higher confidence level means that we are more confident in our statistical analysis and results. However, increasing the confidence level also increases the width of the confidence interval, making it more difficult to detect small effects. Therefore, the choice of the confidence level depends on the context of the study and the goals of the researcher.
- Hypothesized difference: The hypothesized difference refers to the difference in the population parameters between the null hypothesis and the alternative hypothesis. For example, if we want to test whether the mean score on a test is significantly different between two groups (e.g., males and females), the hypothesized difference would be the difference between the mean score of males and the mean score of females.
- Alternative hypothesis: In hypothesis testing, the alternative hypothesis (also called the research hypothesis) is a statement that represents a different conclusion than the null hypothesis. The null hypothesis typically represents the status quo or the assumption that there is no significant difference or relationship between two or more groups or variables. The alternative hypothesis is the statement that is being tested, and it proposes that there is a significant difference or relationship between the groups or variables being studied.
- Assume equal variances: Assuming equal variances in hypothesis testing means that we assume that the variance of the two populations being compared is the same. This assumption is often made when conducting hypothesis tests such as the t-test or ANOVA. When the variances of the two populations are not equal, it can impact the accuracy of the test results. In particular, if the variances are very different, the assumption of equal variances may not hold and using a test that assumes equal variances may lead to incorrect conclusions.
- Individual value plot: An individual value plot is a type of graphical display that can be used in hypothesis testing to visually examine the distribution of a sample of data and compare it to a null hypothesis distribution. It is also sometimes called a dot plot or dot chart. In an individual value plot, each observation in the sample is represented as a single dot on the graph. The horizontal axis typically represents the values of the variable being measured, and the vertical axis shows the frequency or density of the data. Check in will provide you Individual value plot chart or else not.
- Box Plot: Check in will provide you box plot chart or else not.
- Label: This will do the data labels, which contains three options:
- Outlier: Data values that are far away from other data values, can strongly affect your results.
- All quartiles: Quartiles are values that divide a sample of data into four equal parts. Quickly evaluate a data set's spread and central tendency.
- Mean: The mean in a box plot to provide additional information about the data's central tendency.
- Individual Data: An individual data point is a single observation or value in a dataset.
- Download as Excel: This will display the result in an Excel format, which can be easily edited and reloaded for calculations using the load file option.
How to do Two sample t test for summarized data
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/
- On the home page, choose Statistical Tool> Graphical analysis >Two sample t test for summarized data
- Click on Two sample t test for summarized data and reach the dashboard.
- Next, you need to put the values of sample size, sample mean, standard deviation, confidence level and hypothesized difference.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of Two sample t test for summarized data, the window has only left part.
Load File: It is used to directly load the excel data.
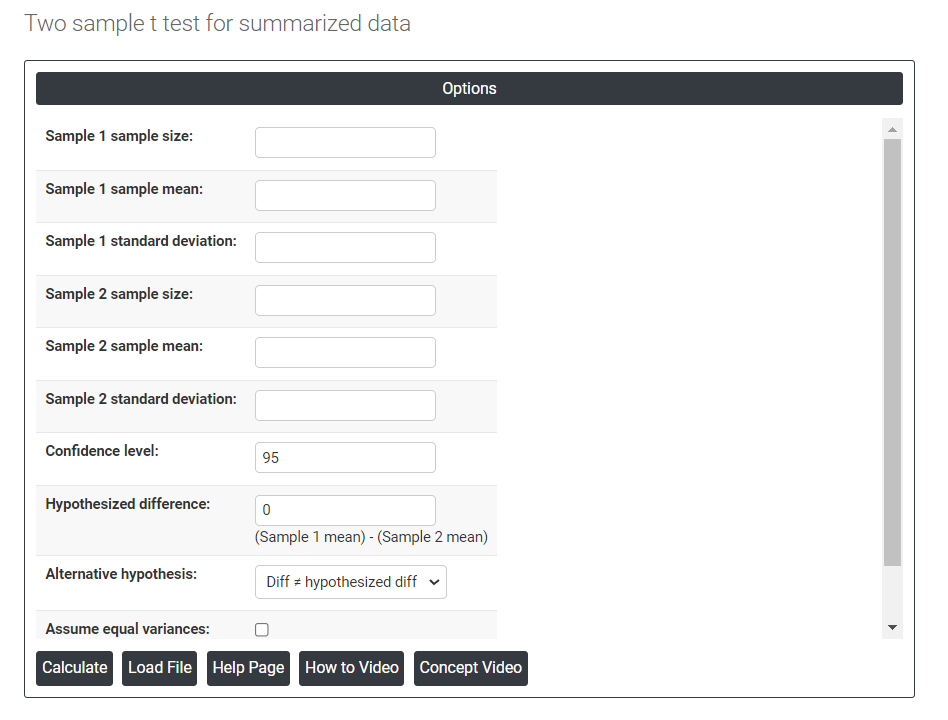
On the left part, there are many options present as follows:
- Sample size: Sample size refers to the number of individuals, objects, or events selected from a population to be studied in order to draw conclusions about the whole population. In other words, it is the number of observations or participants included in a study. The size of the sample can have a significant impact on the accuracy and reliability of the study's results. A larger sample size typically provides a more representative picture of the population and helps to reduce the effects of random sampling error. Therefore, it is important to determine an appropriate sample size before conducting research to ensure that the results are statistically valid and reliable.
- Sample mean: The sample mean is the average value of a set of observations or data points selected from a larger population. It is calculated by adding up all the values in the sample and dividing by the number of observations. The sample mean is often used as an estimator of the population mean, which is the average value of the entire population.
- Sample Standard Deviation: It is a measure of the dispersion or spread of a set of sample data points around their mean. It quantifies how much individual data points deviate from the sample mean.
- Confidence level: In hypothesis testing, the confidence level represents the degree of certainty or level of confidence that we have in our statistical analysis. It is a probability value that indicates the likelihood that the true population parameter falls within the specified range of values. Typically, the confidence level is expressed as a percentage and is denoted by (1 - α), where α is the level of significance or the probability of rejecting a true null hypothesis. For example, if we have a confidence level of 95%, then we are saying that we are 95% confident that the true population parameter lies within our interval estimate, and there is a 5% chance of making a type I error (rejecting a true null hypothesis). In practical terms, a higher confidence level means that we are more confident in our statistical analysis and results. However, increasing the confidence level also increases the width of the confidence interval, making it more difficult to detect small effects. Therefore, the choice of the confidence level depends on the context of the study and the goals of the researcher.
- Hypothesized difference: The hypothesized difference refers to the difference in the population parameters between the null hypothesis and the alternative hypothesis. For example, if we want to test whether the mean score on a test is significantly different between two groups (e.g., males and females), the hypothesized difference would be the difference between the mean score of males and the mean score of females.
- Alternative hypothesis: In hypothesis testing, the alternative hypothesis (also called the research hypothesis) is a statement that represents a different conclusion than the null hypothesis. The null hypothesis typically represents the status quo or the assumption that there is no significant difference or relationship between two or more groups or variables. The alternative hypothesis is the statement that is being tested, and it proposes that there is a significant difference or relationship between the groups or variables being studied.
- Assume equal variances: Assuming equal variances in hypothesis testing means that we assume that the variance of the two populations being compared is the same. This assumption is often made when conducting hypothesis tests such as the t-test or ANOVA. When the variances of the two populations are not equal, it can impact the accuracy of the test results. In particular, if the variances are very different, the assumption of equal variances may not hold and using a test that assumes equal variances may lead to incorrect conclusions.
- Download as Excel: This will display the result in an Excel format, which can be easily edited and reloaded for calculations using the load file. option.