What is One variance test?
One variance test is a statistical hypothesis test used to determine whether the variance of a population is equal to a specified value. It is also called a one-sample variance test because it involves testing a single sample against a known or hypothesized variance.
The one variance test is often used in quality control to ensure that a manufacturing process is producing products with a consistent level of variability. It is also used in research to test whether the variance of a sample is significantly different from a theoretical value or from the variance of another sample.
The most commonly used one variance test is the chi-square test, which is used when the population distribution is unknown and the sample size is relatively large.
When to use One variance test?
Some common scenarios where one variance test is useful include:
- Testing the variance of a sample against a known or hypothesized value: If you have a sample of data and want to test whether the variance of the sample is significantly different from a known or hypothesized value, a one variance test can be used.
- Comparing variances between two samples: If you have two samples of data and want to compare the variances of the two populations, a one variance test can be used to determine whether the difference in variances is statistically significant.
- Checking for heteroscedasticity: One variance test is also used in statistical modeling to check for heteroscedasticity, which occurs when the variance of the errors in a regression model varies systematically across the range of predictor variables.
Guidelines for correct usage of One variance test
- Random sampling should be used to make inferences about a population.
- The sample data should not be severely skewed, and the sample size should be greater than 40 for the Bonett method to perform appropriately. If the data are from a distribution with heavy tails, use caution when interpreting results.
- Each observation should be independent from all other observations.
- The appropriate sample size should be determined so that the estimates have enough precision, the confidence intervals are narrow enough, and there is adequate protection against errors.
- Use the chi-square method only if the data are certain to follow a normal distribution, as even small deviations from normality can greatly affect the results.
Alternatives: When not to use One variance test
- Small sample size: One variance test requires a minimum sample size to ensure statistical power. If the sample size is small, the test may not be reliable, and alternative tests such as the t-test may be more appropriate.
Example of One variance test?
A lumber yard's manager is evaluating the saw mill's efficiency in cutting beams that are meant to be 100 cm long. To do so, the manager takes a sample of 50 beams from the saw mill and measures their lengths. Subsequently, the manager conducts One variance test to determine if the saw mill's standard deviation is significantly different from 1. She has performed the test in following steps:
- She worked all day and gathered the necessary data.
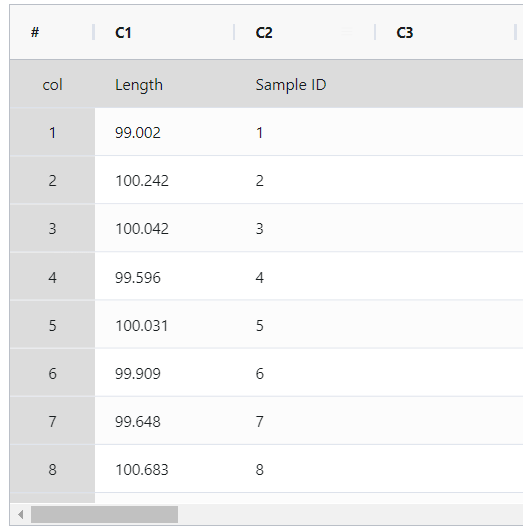
- Now, she analyzes the data with the help of https://qtools.zometric.com/
- Inside the tool, she feeds the data. Also, she puts 95 as the confidence level and hypothesized standard variation as 2.6
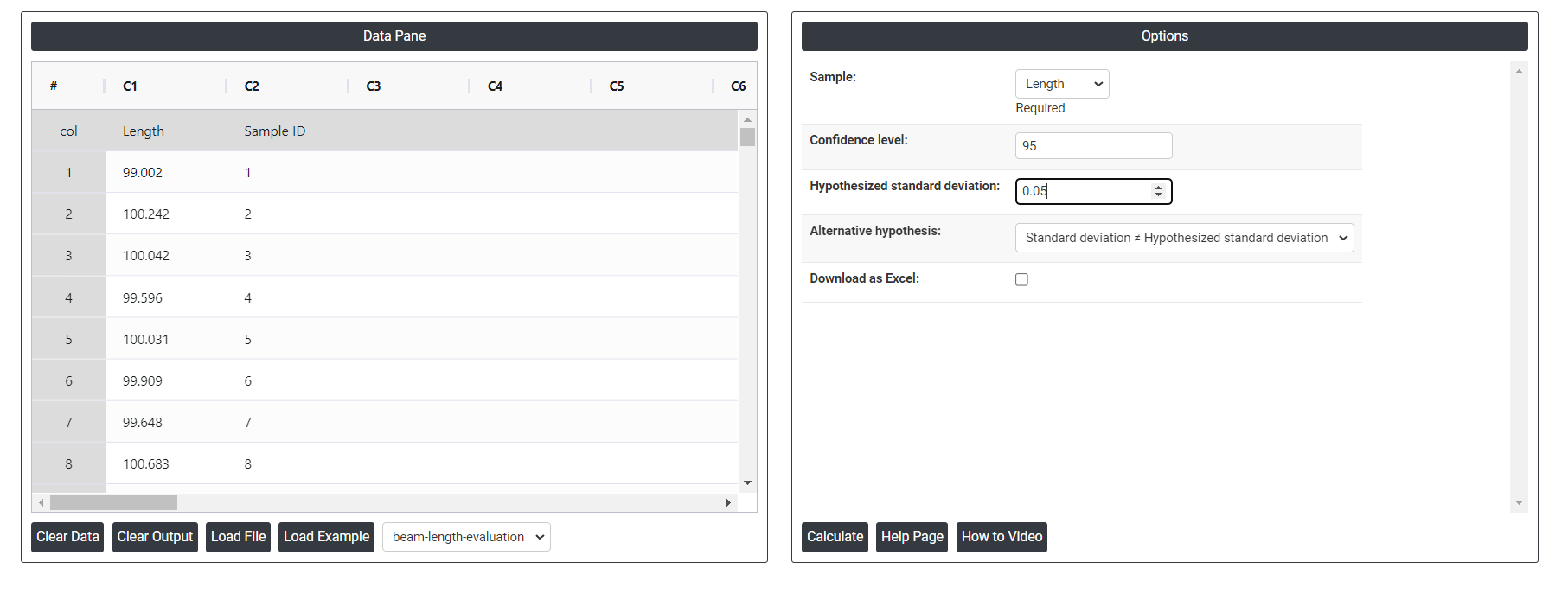
- After using the above mentioned tool, she fetches the output as follows:
How to do One variance test
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/
- On the home page, you can see One variance test under Hypothesis Tests.
- Click on One variance test and reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to put the values of confidence level and hypothesized standard deviation.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of One variance test, the window is separated into two parts.
On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
On the right part, there are many options present as follows:
- Confidence level: In hypothesis testing, the confidence level represents the degree of certainty or level of confidence that we have in our statistical analysis. It is a probability value that indicates the likelihood that the true population parameter falls within the specified range of values. Typically, the confidence level is expressed as a percentage and is denoted by (1 - α), where α is the level of significance or the probability of rejecting a true null hypothesis. For example, if we have a confidence level of 95%, then we are saying that we are 95% confident that the true population parameter lies within our interval estimate, and there is a 5% chance of making a type I error (rejecting a true null hypothesis). In practical terms, a higher confidence level means that we are more confident in our statistical analysis and results. However, increasing the confidence level also increases the width of the confidence interval, making it more difficult to detect small effects. Therefore, the choice of the confidence level depends on the context of the study and the goals of the researcher.
- Hypothesized standard deviation: The hypothesized standard deviation, also known as the assumed standard deviation or the known standard deviation, is the value of the population standard deviation that is assumed to be true for the purpose of a hypothesis test.
- Alternative hypothesis: In hypothesis testing, the alternative hypothesis (also called the research hypothesis) is a statement that represents a different conclusion than the null hypothesis. The null hypothesis typically represents the status quo or the assumption that there is no significant difference or relationship between two or more groups or variables. The alternative hypothesis is the statement that is being tested, and it proposes that there is a significant difference or relationship between the groups or variables being studied.