What is Two variance test?
The two variance test is typically used as a hypothesis test with the null hypothesis that the two samples have equal variances. The test statistic is calculated as the ratio of the sample variances, and its distribution is compared to the F distribution with degrees of freedom based on the sample sizes of the two groups.
When to use Two variance test?
The two-sample variance test is used to determine whether two samples of data have equal variances. It is useful in situations where you want to compare two populations or groups with respect to their variances, such as in the following scenarios:
- Quality control: A manufacturing company may want to compare the variances of two production lines to ensure that they are producing products with consistent quality.
- Clinical trials: Researchers may want to compare the variances of two groups of patients to determine if a new treatment has a similar effect on both groups.
- Education: Educators may want to compare the variances of test scores between two groups of students to see if one group is more consistent than the other.
- Financial analysis: Investors may want to compare the variances of the returns on two different investment portfolios to determine if one is more volatile than the other.
In general, the two-sample variance test is used when you have two samples of data and want to determine if they have equal variances. However, it is important to note that the assumptions of normality and independence should be checked before conducting the test.
Guidelines for correct usage of Two variance test
- Use random samples to make generalizations about the population
- Sample data should not be severely skewed and sample sizes should be >20
- Each observation should be independent from all other observations
- Determine an appropriate sample size to ensure precision, useful confidence intervals, and protection against errors
Alternatives: When not to use Two variance test
- The two-sample variance test is designed for comparing the variances of two independent samples. If your samples are dependent, such as in a before-after study or a matched-pair design, you may need to use a different test such as the paired t-test.
Example of Two variance test?
A consultant in the healthcare industry aims to compare patient satisfaction ratings between two hospitals. In order to do so, the consultant gathers ratings from 20 patients for each hospital and conducts a two-sample variance test to determine if there is a difference in the standard deviations of the patient ratings. She has performed the test in following steps:
- She worked all day and gathered the necessary data.
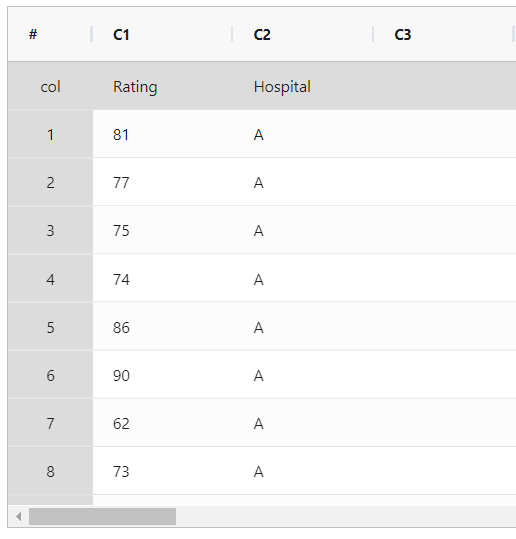
- Now, she analyzes the data with the help of https://qtools.zometric.com/
- Inside the tool, she feeds the data. Also, she puts 95 as the confidence level and hypothesized ratio as 1.
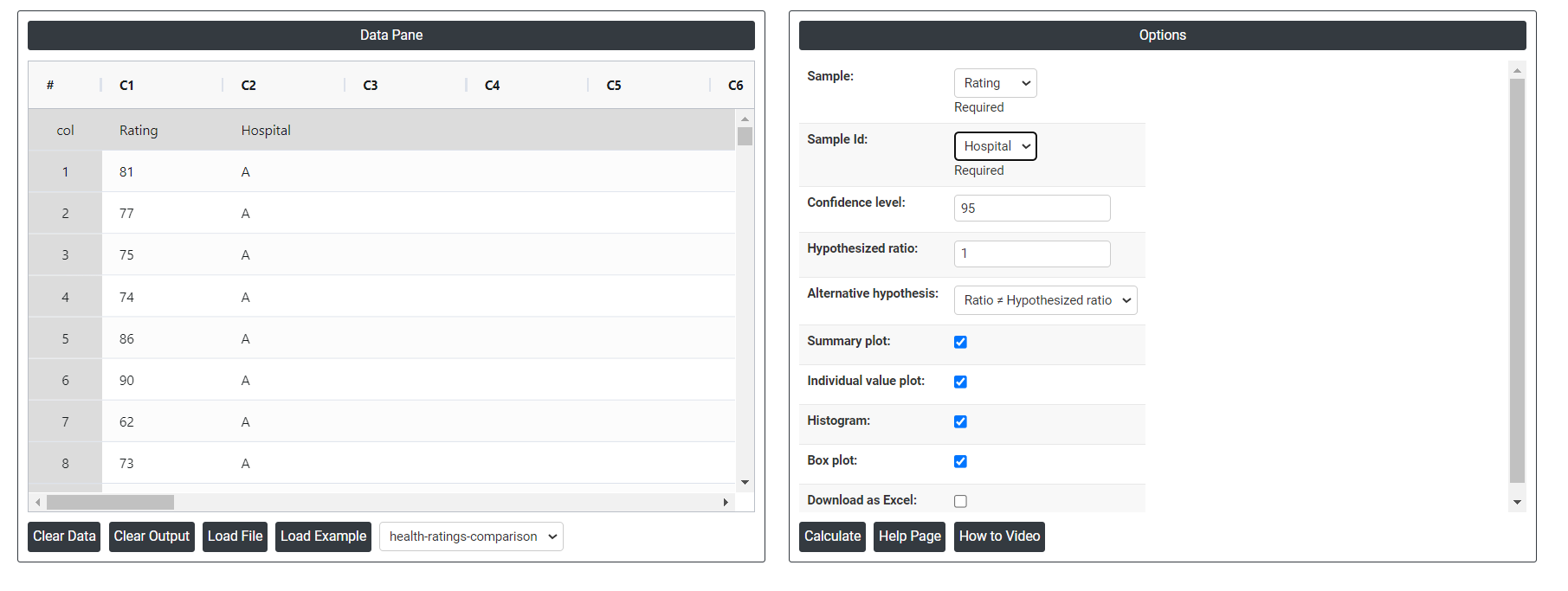
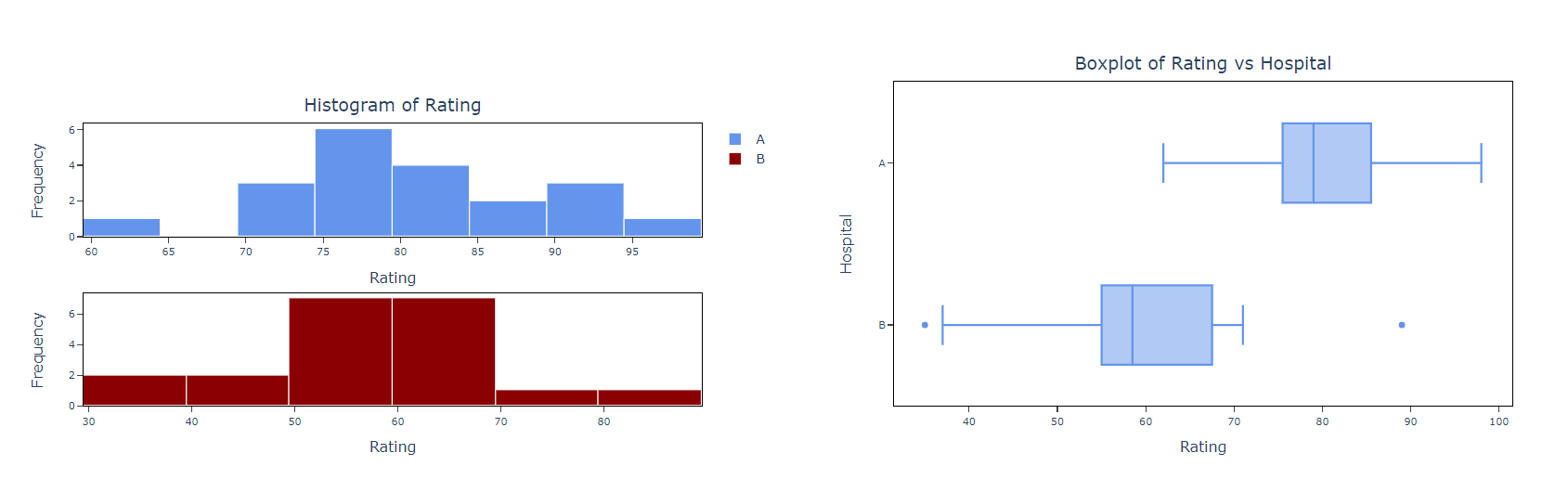
- After using the above mentioned tool, she fetches the output as follows:
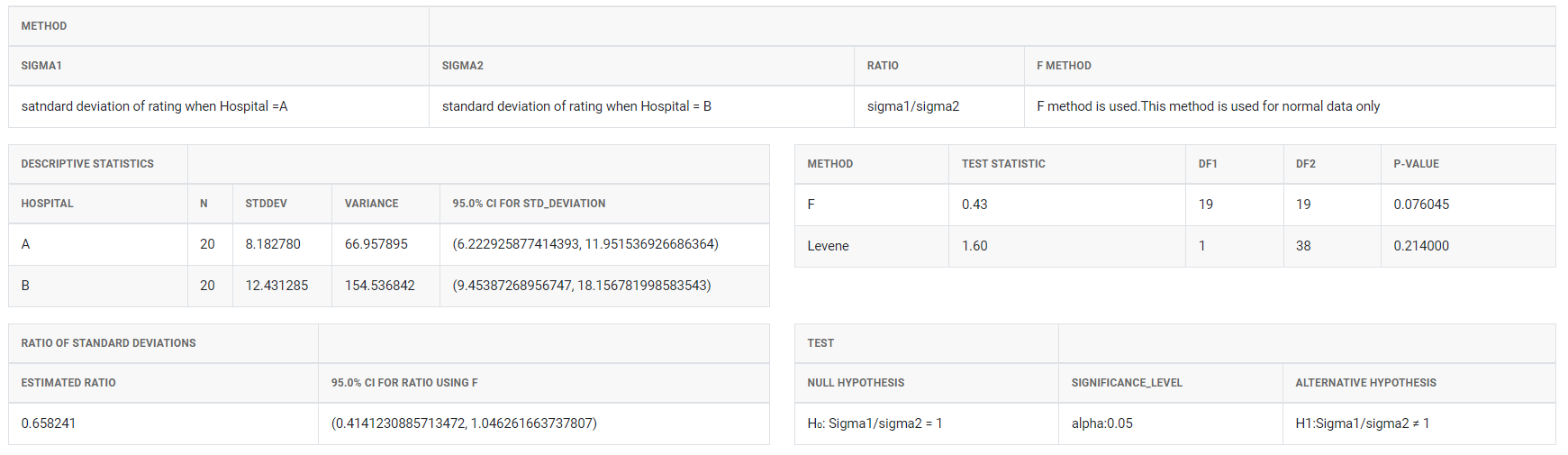
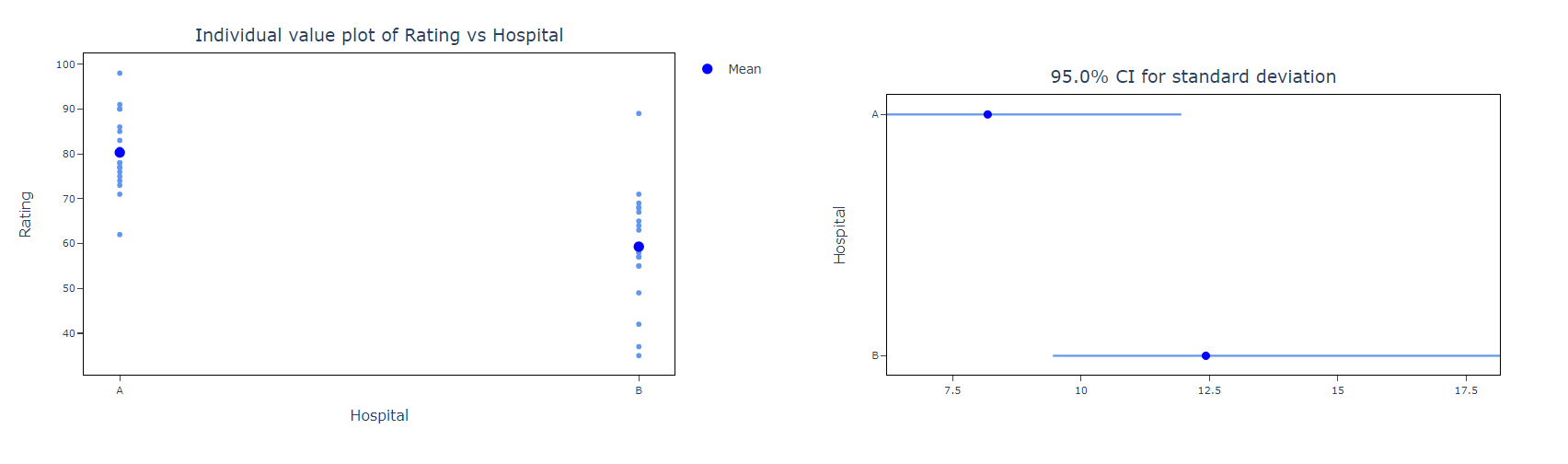
How to do Two variance test
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/
- On the home page, you can see Two variance test under Hypothesis Tests.
- Click on Two variance test and reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to put the values of confidence level and hypothesized rato.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of Two variance test, the window is separated into two parts.
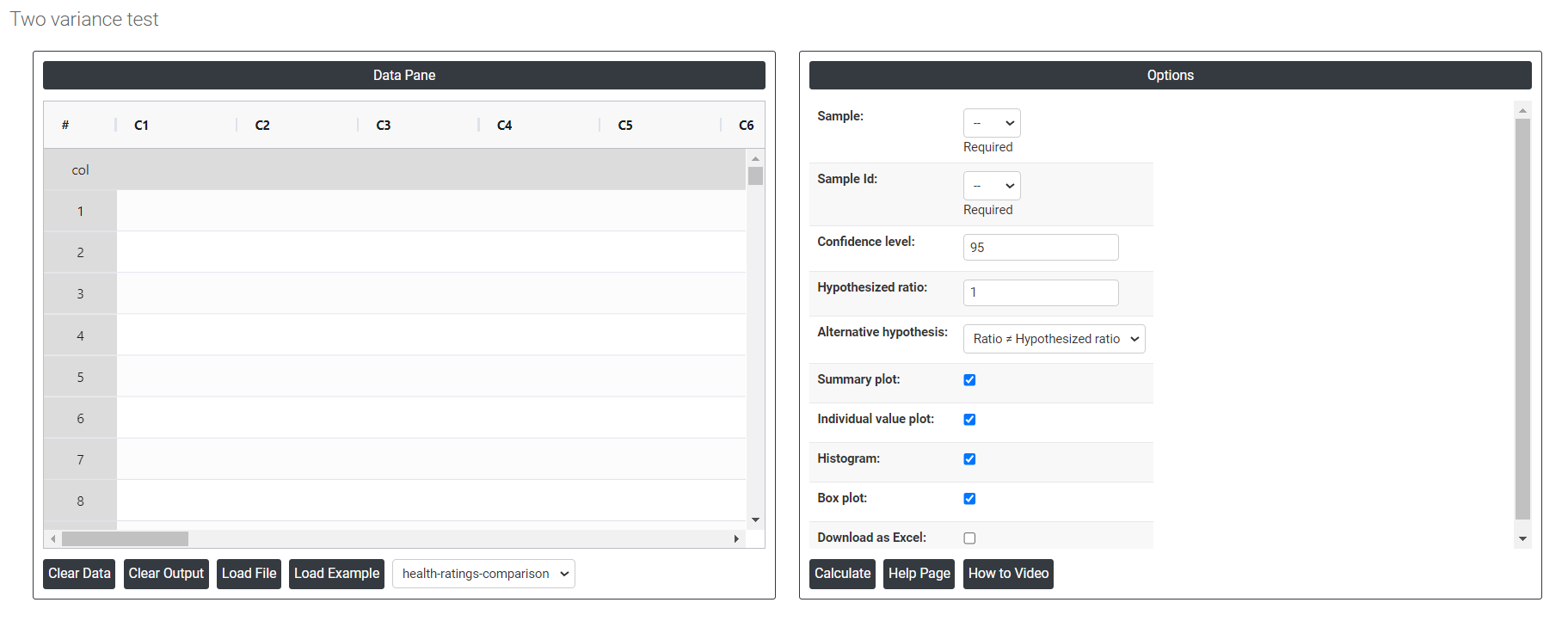
On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
On the right part, there are many options present as follows:
- Confidence level: In hypothesis testing, the confidence level represents the degree of certainty or level of confidence that we have in our statistical analysis. It is a probability value that indicates the likelihood that the true population parameter falls within the specified range of values. Typically, the confidence level is expressed as a percentage and is denoted by (1 - α), where α is the level of significance or the probability of rejecting a true null hypothesis. For example, if we have a confidence level of 95%, then we are saying that we are 95% confident that the true population parameter lies within our interval estimate, and there is a 5% chance of making a type I error (rejecting a true null hypothesis). In practical terms, a higher confidence level means that we are more confident in our statistical analysis and results. However, increasing the confidence level also increases the width of the confidence interval, making it more difficult to detect small effects. Therefore, the choice of the confidence level depends on the context of the study and the goals of the researcher.
- Hypothesized ratio: In a two-variance test, the hypothesized ratio is the value used to test the null hypothesis that the variances of two populations are equal. It represents the expected ratio of the two population variances under the null hypothesis.
- Alternative hypothesis: In hypothesis testing, the alternative hypothesis (also called the research hypothesis) is a statement that represents a different conclusion than the null hypothesis. The null hypothesis typically represents the status quo or the assumption that there is no significant difference or relationship between two or more groups or variables. The alternative hypothesis is the statement that is being tested, and it proposes that there is a significant difference or relationship between the groups or variables being studied.
- Summary plot: The summary plot is useful for quickly visualizing the differences in variance between the two groups being compared. If the variances are similar, the bars will be of similar height, and the horizontal lines will be close together. If the variances differ, the bars will be of different heights, and the horizontal lines will be farther apart. This information can be helpful in interpreting the results of the two-variance test.
- Individual value plot: An individual value plot is a type of graphical display that can be used in hypothesis testing to visually examine the distribution of a sample of data and compare it to a null hypothesis distribution. It is also sometimes called a dot plot or dot chart. In an individual value plot, each observation in the sample is represented as a single dot on the graph. The horizontal axis typically represents the values of the variable being measured, and the vertical axis shows the frequency or density of the data.
- Histogram: In hypothesis testing, a histogram is a graphical representation of the distribution of a sample of data. It is a visual tool used to examine the shape and characteristics of the data. A histogram is created by dividing the data into a set of intervals, or bins, and counting the number of data points that fall into each bin. The bins are typically of equal width, and the height of each bar in the histogram represents the frequency of data points that fall within that bin.
- Box plot: A box plot, also known as a box-and-whisker plot, is a graphical representation of data that displays the distribution of a dataset, including its median, quartiles, and any outliers. In hypothesis testing, a box plot can be used to visually compare the distribution of a sample to a known or expected distribution, such as a normal distribution. This can help determine whether the sample data is significantly different from what is expected. The box in a box plot represents the middle 50% of the data, with the lower edge of the box indicating the first quartile (Q1), the upper edge of the box indicating the third quartile (Q3), and the line inside the box indicating the median. The whiskers extend from the box to the minimum and maximum values in the dataset, excluding any outliers, which are plotted as individual points beyond the whiskers.