Try Statistical Software for Free
What is U Chart?
A u chart, also known as a control chart for defects per unit, is designed to monitor count-type data when the sample size exceeds one. It measures the average number of defects per unit, accommodating both single and multiple types of defects, under the assumption that the data follows a Poisson distribution.
In a u chart, the y-axis shows the number of defects per unit, while the x-axis indicates the number of units or lots. The centerline (u̅) is determined by dividing the total number of defects by the number of inspected items in the sample. This chart is particularly useful for processes where each item can have multiple defects, offering a detailed view of quality over time.
A u chart is essential for monitoring process stability, identifying and correcting any instabilities. It ensures processes stay within control limits and helps detect shifts or trends that could signal issues. By plotting defects per unit, managers can understand variations and address problems swiftly, enhancing overall quality control.
The u chart is applicable in various industries, such as manufacturing, healthcare, and services, to track defects in products, process errors, or incidents over time. It provides a clear visual representation of defect patterns, supporting continuous improvement and decision-making. Accurate records of defects per unit enable organizations to implement strategies that improve process performance and product quality.
When to use U Chart?
A U chart is typically used to analyze data that reflects the count of defects in a set of items. It is particularly useful for assessing the presence of special causes of variation in data. A U chart is used when the sample size is constant and the defects are measured in discrete units. Therefore, it is commonly used in manufacturing processes, quality control, and similar settings where the occurrence of defects needs to be monitored and tracked over time.
Guidelines for correct usage of U Chart
- Count defects on each item or unit, or use P Chart Diagnostic for binary data
- Collect data in time order
- Collect data at appropriate time interval
- Collect data in subgroups that are representative of the process output and subject to the same process conditions
- Subgroups must be large enough to accurately estimate control limits
- Collect enough subgroups to obtain precise control limits
Alternatives: When not to use U chart
If you can determine only whether each item is defective or nondefective, use P Chart to plot the proportion of defective items, or use NP Chart to plot the number of defective items.
Example of U Chart?
A manager for a transcription company wants to evaluate the quality of the transcription service. To do this, the manager randomly selects 25 sets of pages from consecutive orders and counts the number of typographical errors (defects) in each set. Since each set consists of a different number of pages, the manager uses a u chart to monitor the average number of typographical errors per page and assess process stability over time. The manager follows these steps:
- Gathered the necessary data.
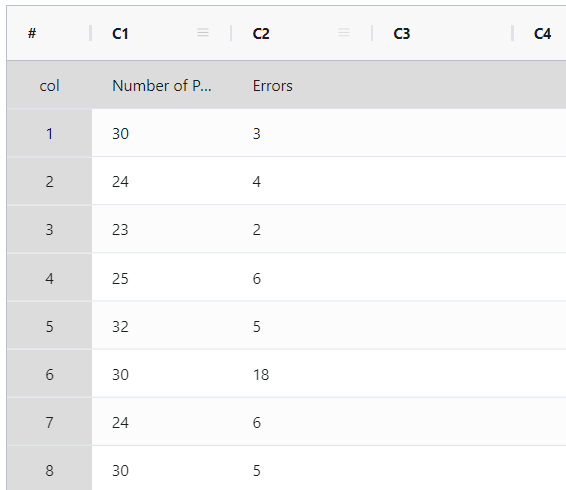
2. Now analyses the data with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/.
3. To find U Chart choose https://intelliqs.zometric.com/> Statistical module> Graphical analysis> U Chart.
4. Inside the tool, feeds the data along with other inputs as follows:
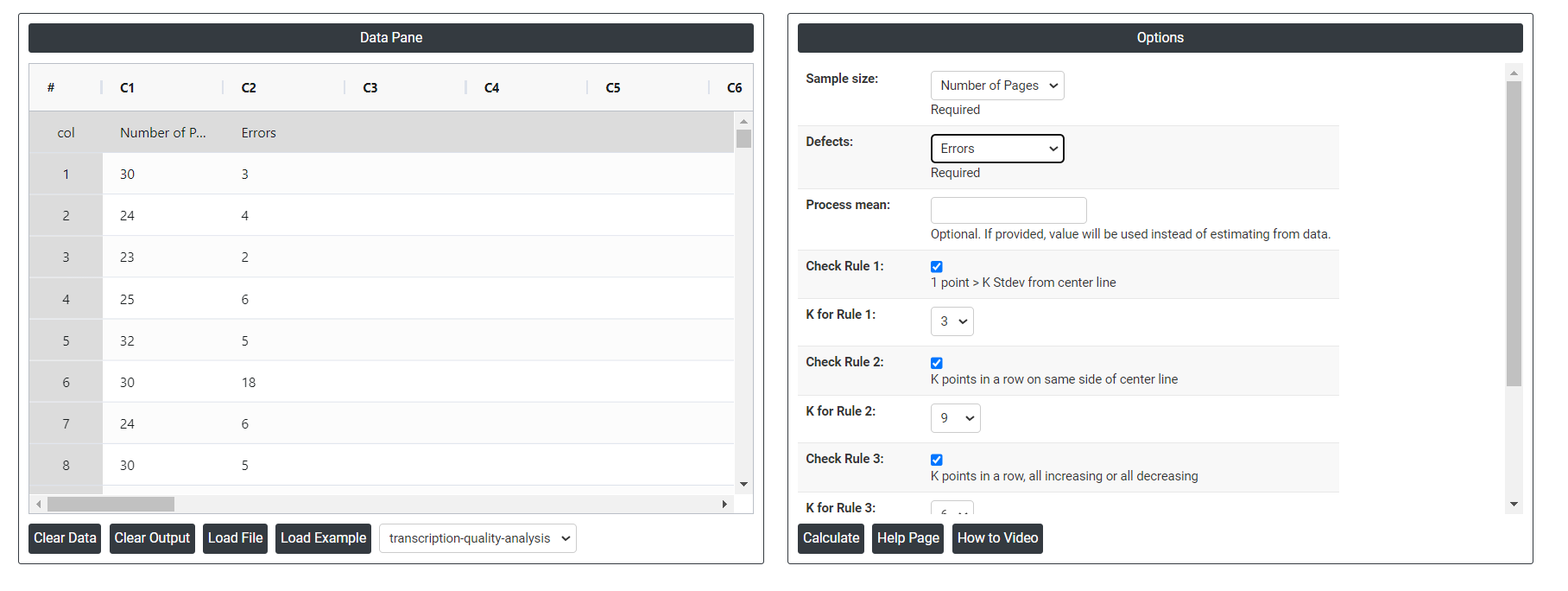
5. After using the above mentioned tool, fetches the output as follows:
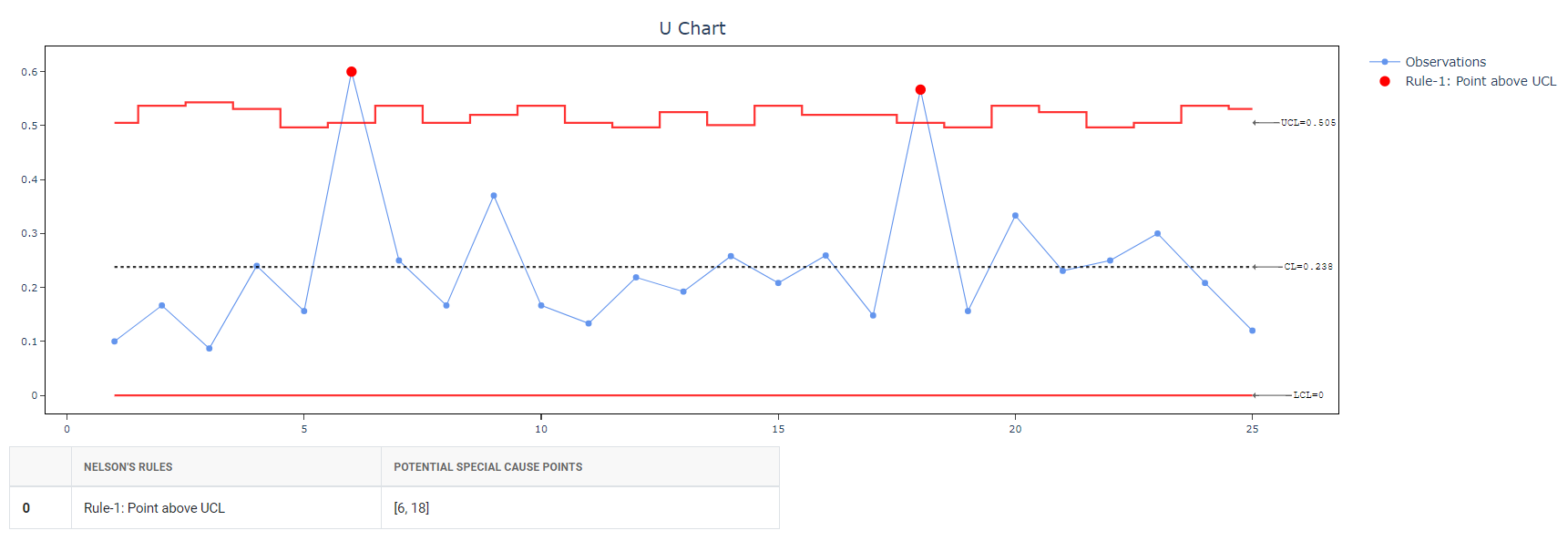
How to generate U Chart?
The guide is as follows:
- Login in to QTools account with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/
- On the home page, choose Statistical Tool> Graphical analysis >U Chart .
- Click on U Chart and will reach the dashboard.
- Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
- Next, you need to select the desired Check Rules.
- Finally, click on calculate at the bottom of the page and you will get desired results.
On the dashboard of U Chart, the window is separated into two parts.
On the left part, Data Pane is present. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
Load example: Sample data will be loaded.
Load File: It is used to directly load the excel data.
On the right part, there are many options present as follows:
- Process proportion: If process proportion is provided, this value is considered to be the centerline. If not, Zometric Q-Tools calculates the centerline from the data provided.
- Check Rule 1: 1 point > K Stdev from center line: Test 1 is essential for identifying subgroups that significantly deviate from others, making it a universally recognized tool for detecting out-of-control situations. To increase sensitivity and detect smaller shifts in the process, Test 2 can be used in conjunction with Test 1, enhancing the effectiveness of control charts.
- Check Rule 2: K points in a row on same side of center line: Test 2 detects changes in process centering or variation. When monitoring for small shifts in the process, Test 2 can be used in conjunction with Test 1 to enhance the sensitivity of control charts.
- Check Rule 3: K points in a row, all increasing or all decreasing: Test 3 is designed to identify trends within a process. This test specifically looks for an extended sequence of consecutive data points that consistently increase or decrease in value, signaling a potential underlying trend in the process behavior.
- Check Rule 4: K points in a row, alternating up and down:Test 4 is designed to identify systematic variations within a process. Ideally, the pattern of variation in a process should be random. However, if a point fails Test 4, it may indicate that the variation is not random but instead follows a predictable pattern.
- Download as Excel: This will display the result in an Excel format, which can be easily edited and reloaded for calculations using the load file option.