Capability Six Pack (Normal) -

What is Capability Six Pack (For Normal)

The Normal Capability Sixpack is a detailed analytical toolset used to assess the performance and capability of a process under the assumption that the data follows a normal distribution. It evaluates process stability and control using control charts and checks for normality with probability plots. The tool estimates both overall (Pp, Ppk) and potential (Cp, Cpk) capability indices, which compare the process spread to specification limits and account for any mean shifts. By specifying lower and/or upper specification limits, the analysis examines the spread of process data relative to these limits to determine if the process is centered and meeting its target. Additionally, it estimates the proportion of products that do not conform to specifications. This thorough analysis helps organizations ensure consistent product quality, identify improvement areas, and confirm process stability and capability.

It is a graphical representation of process capability analysis in Six Sigma methodology. Six Sigma is a quality management approach that aims to identify and reduce process variation to improve efficiency and minimize defects.

A Capability Sixpack, also known as a Capability Analysis Sixpack or a Capability Analysis Report, consists of a set of six plots or charts that provide a comprehensive view of process capability. These charts are used to assess whether a process meets customer specifications and to identify areas for improvement.

When to use Capability Six Pack

Here are some situations where a Capability Sixpack can be useful:

Process Improvement: When you are implementing process improvement initiatives or trying to reduce process variation, a Capability Sixpack can help you understand the current state of the process and identify areas that need improvement.
New Process Validation: If you are introducing a new process or making significant changes to an existing process, a Capability Sixpack can be used to evaluate the process's initial capability and assess its ability to meet customer requirements.
Continuous Monitoring: A Capability Sixpack can be employed as part of ongoing process monitoring efforts to ensure that the process remains within acceptable limits and meets customer specifications over time. Regular monitoring using the Capability Sixpack can help detect any process shifts or variations that may impact quality.
Supplier Evaluation: When evaluating potential suppliers or assessing the capability of existing suppliers, a Capability Sixpack can be used to determine if the supplier's process is capable of consistently producing products that meet your specifications.

Guidelines for correct usage of Capability Six Pack

Ensure that the data is continuous and suitable for analysis.
For attribute data (counts of defectives or defects), use Binomial or Poisson Capability Analysis.
Collect a sufficient amount of data (at least 100 total data points) to obtain reliable estimates of process capability.
Collect data in rational subgroups that are representative of the process and collected under similar conditions.
Verify that the process is stable and in control using control charts in the capability sixpack output.
The data should follow a normal distribution for accurate process capability estimates.
If the data are non-normal, consider transforming them using Box-Cox or Johnson transformations.
Use the normal probability plot and histogram in the capability sixpack output to assess data distribution.

Alternatives: When not to use Capability Six Pack

If you desire a comprehensive evaluation of capability measures, including the main indices, consider employing Normal Capability Analysis.
To assess the assumptions necessary for nonnormal capability analysis, utilize Nonnormal Capability Sixpack.
In the case of substantial variation between subgroups, such as in a batch process, use Between/Within Capability Sixpack to evaluate the assumptions for a between/within capability analysis.

Example of Capability Six Pack (Normal)

The quality engineer at an automotive parts plant is evaluating the process capability of the machine used to produce camshafts. The engineer collects data in subgroups of size 5 every 30 minutes from one of the machines. The specified limits for camshaft length are a Lower Specification Limit (LSL) of 595 mm, a Target of 600 mm, and an Upper Specification Limit (USL) of 605 mm. To assess the assumptions necessary for normal capability analysis and determine how well the camshaft lengths meet the specified requirements, the engineer conducts a normal capability sixpack analysis. The following steps:

Gathered the necessary data.

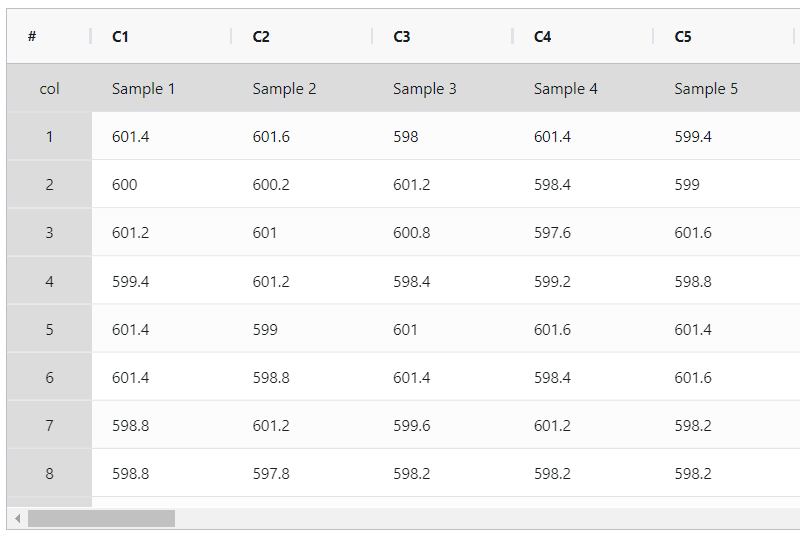
Now analyses the data with the help of https://qtools.zometric.com/or https://intelliqs.zometric.com/.
To find Capability Six Pack choose https://intelliqs.zometric.com/> Statistical module> Graphical analysis>Capability Six Pack.
Inside the tool, feeds the data along with other inputs as follows:

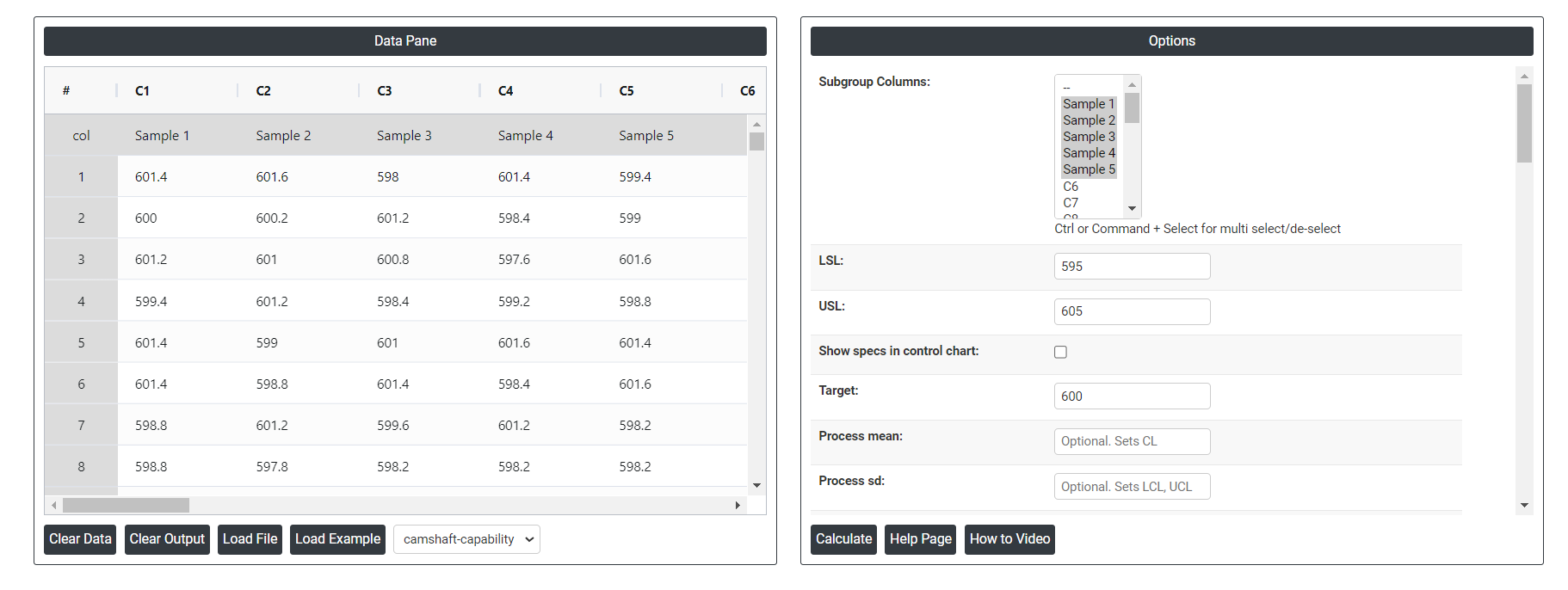
After using the above mentioned tool, fetches the output as follows:

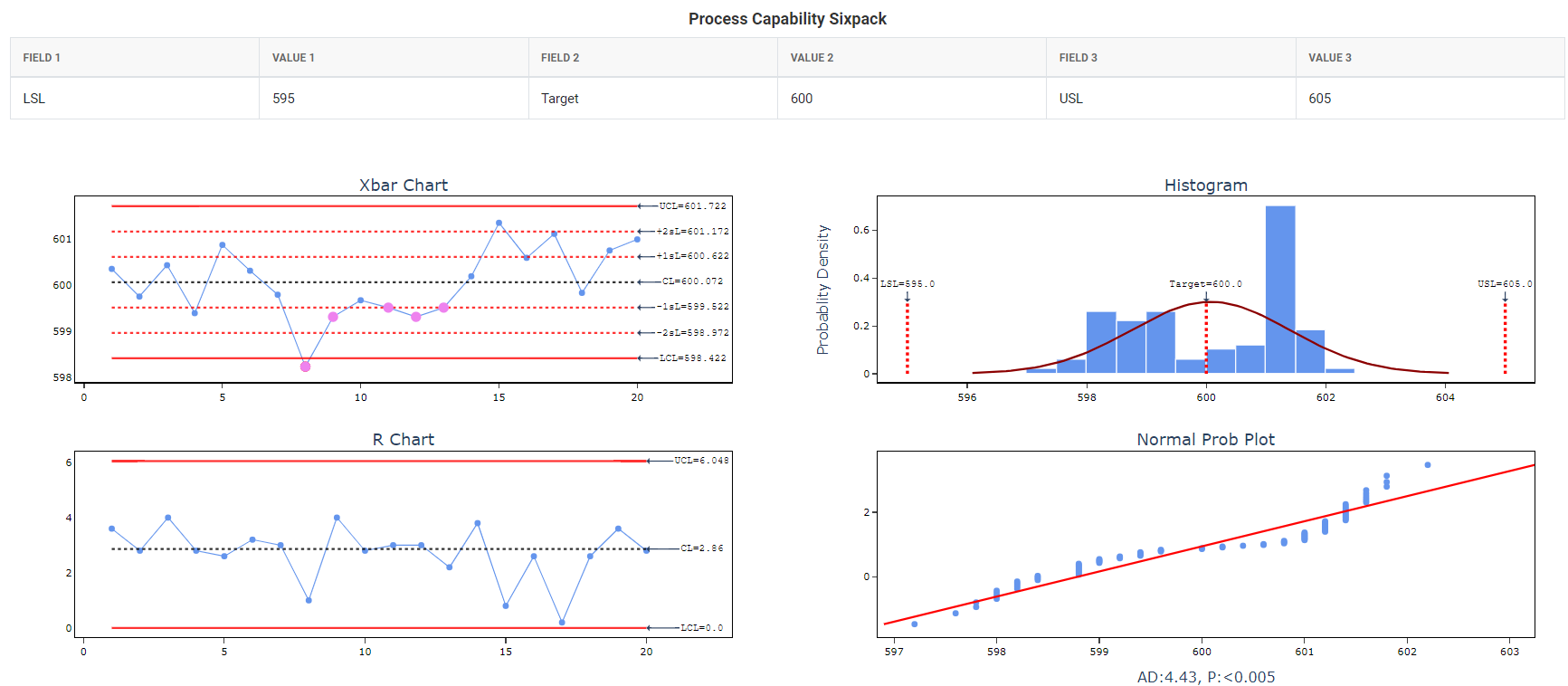
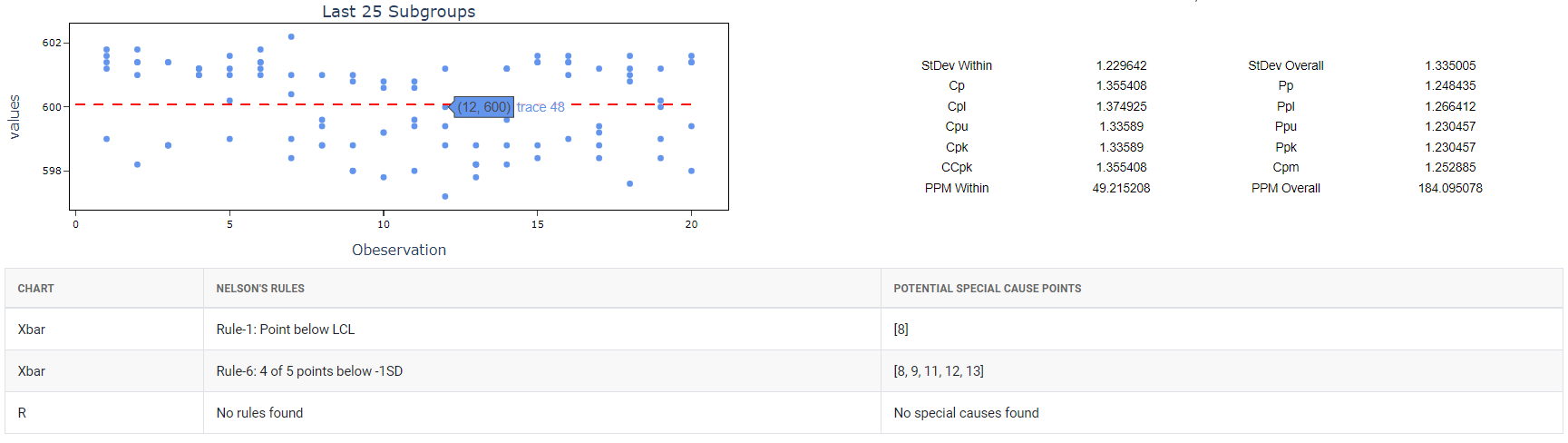
How to do Capability Six Pack (Normal)

The guide is as follows:

Login in to QTools account with the help of https://qtools.zometric.com/ or https://intelliqs.zometric.com/
On the home page, choose Statistical Tool> Graphical analysis >Capability Six Pack (Normal) .
Click on Capability Six Pack (Normal) and reach the dashboard.
Next, update the data manually or can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.
Next, you need to fill the desired details such as lsl, usl, target, K, etc.
Finally, click on calculate at the bottom of the page and you will get desired results.

On the dashboard of Capability Six Pack (Normal), the window is separated into two parts.

On the left part, Data Pane is present. In the Data Pane, each row makes one subgroup. Data can be fed manually or the one can completely copy (Ctrl+C) the data from excel sheet and paste (Ctrl+V) it here.

Load example: Sample data will be loaded.

Load File: It is used to directly load the excel data.

On the right part, there are many options present as follows:

Lsl: LSL in process capability refers to the Lower Specification Limit. It is the lower boundary or threshold set for a specific process parameter or characteristic. In process capability analysis, LSL is used to determine whether a process is capable of producing outputs within the desired range or specifications.
Usl: USL in process capability refers to the Upper Specification Limit. It represents the upper boundary or threshold set for a specific process parameter or characteristic. During process capability analysis, the USL is used to assess whether a process is capable of producing outputs within the desired range or specifications.
Target: In process capability, the target refers to the desired or ideal value for a specific process parameter or characteristic. It represents the value that the process is intended to achieve or center around. The target is often based on design specifications or customer requirements.
Show specs in control chart: Adding specification limits to the control chart to visualize how process measurements align with quality standards. This helps in assessing whether the process remains within acceptable ranges.
Process mean: It is the average value of a set of measurements or observations from a process. It represents the central tendency of the process data over time and is a key indicator of the process performance. If not, Zometric Q-Tools calculates the centerline from the data provided.
Process sd: It is a measure of the variability or dispersion of the process data around the mean. It provides an indication of how much individual data points within the process differ from the process average. If not, Zometric Q-Tools calculates from the data provided.
K: In process capability, K refers to the process capability index known as the "Process Capability Index for Non-Centered Distribution" or simply the K-index. It is used to evaluate the capability of a process in relation to the specification limits.
Within Stdev estimation method:
- Pooled: The pooled standard deviation is the weighted average of subgroup variances, with larger subgroups having a greater impact on the overall estimate. This method offers a more accurate estimate of the standard deviation when the process is stable.
- Rbar: Rbar represents the average of the ranges within subgroups. The Rbar method is a widely used estimate of the standard deviation, particularly effective for subgroup sizes ranging from 2 to 8.
- Sbar:It calculates the average standard deviation (Sbar) of subgroups to monitor process variability. Sbar is crucial for setting control limits on the S chart, indicating changes in data dispersion over time. This method ensures consistent and accurate assessment of process variation in quality control practices.
Within stdev estimation method for subgroup size = 1:
- Average Moving Range: The average moving range is the mean value of the range of two or more consecutive points, typically used when the subgroup size is 1.
- Median Moving Range: The median moving range is the middle value of the range of two or more consecutive points, recommended when data have extreme ranges that could skew the moving range.
Moving range of length: Specify the number of observations used to compute the moving range, with the length being ≤ 100. The default length is 2, as consecutive values are most likely to be similar.
Use Unbiasing Constants to Calculate Overall Standard Deviation: Apply unbiasing constants in estimating the overall standard deviation.
Machine: The specific equipment or machinery being evaluated in the capability study. Example: Drilling machine, forging machine.
Reported by: The person who documents the results of the capability study.
Prepared by: The individual who compiles and organizes the data for the report.
Verified by: The person who checks the accuracy of the compiled data and findings.
Approved by: The individual who authorizes the final report for distribution or use.
Remarks: Additional notes or observations relevant to the study that may affect interpretation.
Shift: The work shift during which the study was performed, indicating timing and possible shift-specific variables.
Operation: The specific process or machine being assessed in the study.
Company name: The organization conducting the capability study.
Report title: The title summarizing the focus or purpose of the capability study.
Customer name: The client or customer for whom the capability study was conducted.
Part: The component or product name or number being manufactured by the machine.
Variable: The specific characteristic or dimension of the part being measured. Example: Diameter, length, width.
Unit of Measure: The units used to quantify the variable being measured. Example: Millimeters (mm), inches (in).
Study date: The date on which the machine capability study was conducted.
Operator: The name of the machine being operated.
Inspector: The name of the tool or instrument used for measuring. Example: "Micrometer Model Y."
Gauge: The measurement instrument or tool used to assess the variable. Example: Caliper, micrometer.
Check Rule 1: 1 point > K Stdev from center line: Test 1 is essential for identifying subgroups that significantly deviate from others, making it a universally recognized tool for detecting out-of-control situations. To increase sensitivity and detect smaller shifts in the process, Test 2 can be used in conjunction with Test 1, enhancing the effectiveness of control charts.
Check Rule 2: K points in a row on same side of center line: Test 2 detects changes in process centering or variation. When monitoring for small shifts in the process, Test 2 can be used in conjunction with Test 1 to enhance the sensitivity of control charts.
Check Rule 3: K points in a row, all increasing or all decreasing: Test 3 is designed to identify trends within a process. This test specifically looks for an extended sequence of consecutive data points that consistently increase or decrease in value, signaling a potential underlying trend in the process behavior.
Check Rule 4: K points in a row, alternating up and down: Test 4 is designed to identify systematic variations within a process. Ideally, the pattern of variation in a process should be random. However, if a point fails Test 4, it may indicate that the variation is not random but instead follows a predictable pattern.
Check Rule 5: K out of K + 1 points > 2 standard deviation from center line (same side): Test 5 detects small shifts in the process.
Check Rule 6: K out of K + 1 points > 1 standard deviation from center line (same side):Test 6 detects small shifts in the process.
Check Rule 7: K points in a row within 1 standard deviation of center line (either side):Test 7 identifies patterns of variation that may be incorrectly interpreted as evidence of good control. This test detects overly wide control limits, which are often a result of stratified data. Stratified data occur when there is a systematic source of variation within each subgroup, causing the control limits to appear broader than they should be.
Check Rule 8: K points in a row > 1 standard deviation from center line (either side):Test 8 detects a mixture pattern. In a mixture pattern, the points tend to fall away from the center line and instead fall near the control limits.
Download as Excel: This will display the result in an Excel format, which can be easily edited and reloaded for calculations using the load file option.

Try Statistical Software for Free